《2025年5年中考3年模拟九年级数学上册沪科版》

1.「2025安徽合肥庐阳中学月考」$2\sin 30^{\circ }$的值等于( )

A.1
B.$\sqrt {2}$
C.$\sqrt {3}$
D.2

答案： A 2sin30°=2×$\frac{1}{2}$=1.故选A.

2.「2024天津中考」$\sqrt {2}\cos 45^{\circ }-1$的值等于( )

A.0
B.1
C.$\frac {\sqrt {2}}{2}-1$
D.$\sqrt {2}-1$

答案： A $\sqrt{2}$cos45°-1=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-1=1-1=0.故选A.

3.「2025宁夏银川外国语实验学校月考」已知实数$a= \tan 30^{\circ },b= \cos 60^{\circ },c= \sin 45^{\circ }$,则下列判断正确的是( )

A.$b＞a＞c$
B.$c＞a＞b$
C.$b＞c＞a$
D.$a＞c＞b$

答案： B
∵a=tan30°=$\frac{\sqrt{3}}{3}$,b=cos60°=$\frac{1}{2}$,c=sin45°=$\frac{\sqrt{2}}{2}$,且$\frac{\sqrt{2}}{2}$＞$\frac{\sqrt{3}}{3}$＞$\frac{1}{2}$,
∴c＞a＞b.故选B.

4. 若一个三角形三个内角度数的比为$1:2:3$,那么这个三角形最小内角的正切值为( )

A.$\frac {\sqrt {3}}{3}$
B.$\frac {1}{2}$
C.$\frac {1}{3}$
D.$\frac {\sqrt {3}}{2}$

答案： A 设三个内角的度数分别为x,2x,3x,则x+2x+3x=180°,解得x=30°,即最小内角的度数为30°,tan30°=$\frac{\sqrt{3}}{3}$.故选A.

5. 学科特色教材变式P118T2 计算：
(1)$2\sin 30^{\circ }+3\cos 60^{\circ }-4\tan 45^{\circ }.$
(2)$\frac {\cos ^{2}30^{\circ }}{1+\sin 30^{\circ }}+\tan ^{2}60^{\circ }.$
(3)$3\tan 30^{\circ }-\frac {1}{\cos 60^{\circ }}+\sqrt {8}\cos 45^{\circ }+\sqrt {(1-\tan 60^{\circ })^{2}}.$

答案： 解析
(1)原式=2×$\frac{1}{2}$+3×$\frac{1}{2}$-4×1=1+$\frac{3}{2}$-4=-$\frac{3}{2}$.
(2)原式=$\frac{(\frac{\sqrt{3}}{2})^{2}}{1+\frac{1}{2}}$+($\sqrt{3}$)²=$\frac{\frac{3}{4}}{\frac{3}{2}}$+3=$\frac{7}{2}$.
(3)原式=3×$\frac{\sqrt{3}}{3}$-$\frac{1}{\frac{1}{2}}$+$\sqrt{8}$×$\frac{\sqrt{2}}{2}$+$\sqrt{(1-\sqrt{3})^{2}}$=$\sqrt{3}$-2+2+$\sqrt{3}$-1=2$\sqrt{3}$-1.

6.「2024安徽合肥滨湖寿春中学月考」若锐角A满足$\cos A= \frac {\sqrt {3}}{2}$,则$∠A$的度数是( )

A.$15^{\circ }$
B.$30^{\circ }$
C.$45^{\circ }$
D.$60^{\circ }$

答案： B
∵锐角A满足cosA=$\frac{\sqrt{3}}{2}$,
∴∠A的度数是30°.故选B.

7.「2025安徽淮北二中月考」若$\sin (x+15^{\circ })= \frac {\sqrt {3}}{2}$,则锐角$x= $______$^{\circ }$。

答案： 答案 45
解析
∵sin(x+15°)=$\frac{\sqrt{3}}{2}$,
∴x+15°=60°,
∴x=45°.

8.「2024吉林松原长岭期末」在$\triangle ABC$中,$|\cos A-\frac {1}{2}|+(1-\tan B)^{2}= 0$,求$∠A,∠B,∠C$的度数。

答案： 解析
∵|cosA-$\frac{1}{2}$|+(1-tanB)²=0,
∴cosA-$\frac{1}{2}$=0,1-tanB=0,
∴cosA=$\frac{1}{2}$,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°-∠A-∠B=180°-60°-45°=75°.

9. 学科特色多解法「2023湖南益阳中考,★☆」如图,在平面直角坐标系xOy中,有三点$A(0,1),B(4,1),C(5,6)$,则$\sin ∠BAC= $( )


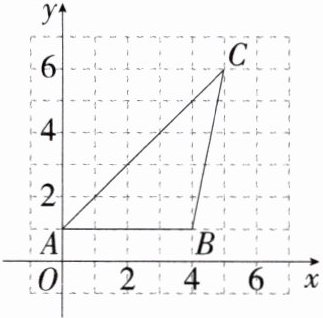
A.$\frac {1}{2}$
B.$\frac {\sqrt {13}}{5}$
C.$\frac {\sqrt {2}}{2}$
D.$\frac {\sqrt {3}}{2}$

答案： C 【解法一】由题图可知,∠BAC=45°,
∴sin∠BAC=sin45°=$\frac{\sqrt{2}}{2}$.故选C.
【解法二】过C作CD⊥AB交AB的延长线于D,图略,
∵A(0,1),B(4,1),C(5,6),
∴D(5,1),
∴CD=6-1=5,AD=5,
∴AC=5$\sqrt{2}$,
∴sin∠BAC=$\frac{CD}{AC}$=$\frac{\sqrt{2}}{2}$,故选C.