《2025年5年中考3年模拟九年级数学上册沪科版》

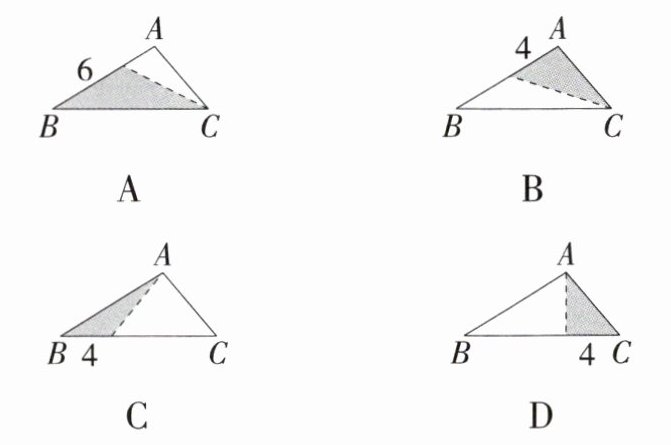
7.新 考向 「2025安徽合肥五十五中期中,」下列选项的三角形纸片ABC中,$AB= 9,AC= 6,BC= 12$,沿虚线剪下的阴影部分的三角形与$\triangle ABC$相似的是( )

答案： B　在三角形纸片ABC中,AB=9,AC=6,BC=12.A.因为$\frac{6}{BC}=\frac{6}{12}=\frac{1}{2}$,$\frac{AB}{BC}=\frac{9}{12}=\frac{3}{4}$,$\frac{1}{2}\neq\frac{3}{4}$,所以沿虚线剪下的阴影部分的三角形与△ABC不相似，故A选项不符合题意;B.因为$\frac{4}{AC}=\frac{4}{6}=\frac{2}{3}$,$\frac{AC}{AB}=\frac{6}{9}=\frac{2}{3}$,且∠A=∠A,所以沿虚线剪下的阴影部分的三角形与△ABC相似，故B选项符合题意;C.因为$\frac{4}{AB}=\frac{4}{9}$,$\frac{AB}{BC}=\frac{9}{12}=\frac{3}{4}$,$\frac{4}{9}\neq\frac{3}{4}$,所以沿虚线剪下的阴影部分的三角形与△ABC不相似，故C选项不符合题意;D.因为$\frac{4}{AC}=\frac{4}{6}=\frac{2}{3}$,$\frac{AC}{BC}=\frac{6}{12}=\frac{1}{2}$,$\frac{2}{3}\neq\frac{1}{2}$，所以沿虚线剪下的阴影部分的三角形与△ABC不相似,故D选项不符合题意.故选B.

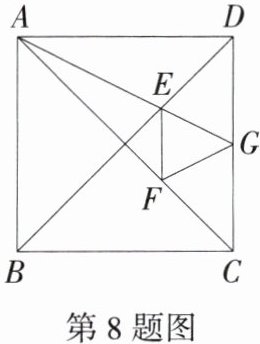
8.「2024山东烟台中考,」如图,在正方形ABCD中,点E,F分别为对角线BD,AC的三等分点,连接AE并延长交CD于点G,连接EF,FG.若$∠AGF= α$,则$∠FAG$用含α的代数式表示为( )

A.$\frac {45^{\circ }-α}{2}$
B.$\frac {90^{\circ }-α}{2}$
C.$\frac {45^{\circ }+α}{2}$
D.$\frac {α}{2}$

答案： B　设AC与BD的交点为O,
∵四边形ABCD为正方形，点E,F分别为对角线BD,AC的三等分点，
∴AB//CD,AB=CD,OD=OC,∠ODC=∠OCD=45°,DE=CF,$\frac{DE}{BE}=\frac{1}{2}$,
∴OE=OF.
∵∠EOF=∠DOC,$\frac{OE}{OD}=\frac{OF}{OC}$,
∴△EOF∽△DOC,
∴∠OFE=∠OCD=45°.
∵AB//DC,
∴△ABE∽△GDE,
∴$\frac{DG}{AB}=\frac{DE}{BE}=\frac{1}{2}$,
∴DG=$\frac{1}{2}$AB=$\frac{1}{2}$CD=CG,
∴△DEG≌△CFG(SAS),
∴GE=GF,
∴∠GEF=$\frac{1}{2}(180° - ∠AGF)=90° - \frac{1}{2}\alpha$,
∴∠FAG=∠GEF - ∠AFE=$90° - \frac{α}{2} - 45°=45° - \frac{α}{2}=\frac{90° - α}{2}$,故选B.

9.学科 易错题「2025安徽六安霍邱期中改编,」如图,$AB⊥BD$于点B,$CD⊥BD$于点D,$AB= 6,CD= 4,BD= 14$.点P在BD上移动,当BP的长为____时,以P,C,D为顶点的三角形与以P,A,B为顶点的三角形相似.

答案： 答案　$8.4$或$2$或$12$
　解析　设DP=x,则BP=BD - DP=14 - x.
∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°.当$\frac{AB}{CD}=\frac{BP}{DP}$时,△ABP∽△CDP,即$\frac{6}{4}=\frac{14 - x}{x}$,解得$x=\frac{28}{5}$,
∴BP=14 - $\frac{28}{5}=8.4$.当$\frac{AB}{DP}=\frac{BP}{DC}$时,△ABP∽△PDC,即$\frac{6}{x}=\frac{14 - x}{4}$,整理得$x^2 - 14x + 24=0$,解得$x_1=2$,$x_2=12$,
∴BP=14 - 2=12或BP=14 - 12=2.综上,当BP的长为$8.4$或$2$或$12$时,以P,C,D为顶点的三角形与以P,A,B为顶点的三角形相似.
易错警示　本题容易因为考虑问题不全面，漏掉AB与PD对应的情况，导致漏解.

10.「2025安徽蚌埠期中,」如图,在矩形ABCD中,点E是边CD上任意一点(点E与点C,D不重合),过点A作$AF⊥AE$,交边CB的延长线于点F,连接EF交边AB于点G,连接AC.
(1)求证:$\triangle AEF\backsim \triangle DAC$.
(2)如果FE平分$∠AFB$,连接CG,求证:四边形AGCE为菱形.

答案： 证明　
(1)
∵四边形ABCD是矩形,
∴AB//CD,AB=DC,∠BCD=∠DAB=∠ABC=∠D=90°,
∴∠ABF=180° - ∠ABC=90°.
∵AE⊥AF,
∴∠FAE=90°,
∴∠FAE - ∠BAE=∠DAB - ∠BAE,
∴∠BAF=∠DAE.又
∵∠D=∠ABF=90°,
∴△ABF∽△ADE,
∴$\frac{AB}{AD}=\frac{AF}{AE}$,
∴$\frac{DC}{AD}=\frac{AF}{AE}$,
∴$\frac{DC}{AF}=\frac{AD}{AE}$.又
∵∠D=∠FAE=90°,
∴△AEF∽△DAC.
(2)
∵FE平分∠AFB,
∴∠AFE=∠CFE.
∵∠FAE=∠BCD=90°,EF=EF,
∴△AFE≌△CFE(AAS),
∴AF=CF,AE=EC.
∵FG=FG,
∴△AFG≌△CFG(SAS),
∴∠FAG=∠FCG.
∵∠BAF=∠DAE,
∴∠DAE=∠FCG.
∵∠DAE + ∠AED=90°,∠BCG + ∠DCG=90°,
∴∠DCG=∠AED,
∴AE//CG.
∵AB//CD,
∴四边形AGCE是平行四边形.又
∵AE=EC,
∴四边形AGCE为菱形.

11.新 课标 推理能力 问题探究:
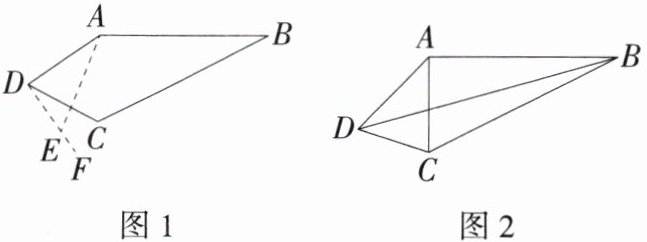
(1)如图1,在四边形ABCD中,$∠ABC与∠ADC$互余,小明发现四边形ABCD中这对互余的角可进行拼合:作$∠CDF= ∠ABC$,在射线DF上任取一点E(不与点D重合),连接AE,发现AD,DE,AE之间的数量关系是____.
问题解决:
(2)如图2,有一个四边形公园ABCD,B,D是公园的两个入口,AC和BD是公园的两条主干道,其中$∠BAC= 90^{\circ },∠ABC与∠ADC$互余,$AB= 2AC,AD= 100m,CD= 70m$,求BD的长.

答案：
解析　
(1)$AD^2 + DE^2=AE^2$.
(2)如图,在线段DC的下方作∠CDT=∠ABC,过点C作CT⊥DT于T,连接AT,则∠CTD=∠CAB=90°,
∵∠CDT=∠ABC,
∴△CTD∽△CAB,
∴∠DCT=∠ACB,$\frac{CD}{CB}=\frac{CT}{CA}$,
∴$\frac{CD}{CT}=\frac{CB}{CA}$,∠DCB=∠TCA,
∴△DCB∽△TCA,
∴$\frac{BD}{AT}=\frac{CB}{CA}$.
∵AB=2AC,
∴AC:AB:BC=CT:DT:CD=1:2:$\sqrt{5}$,
∴$\frac{BD}{AT}=\frac{CB}{CA}=\frac{\sqrt{5}}{1}$,$\frac{DT}{CD}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$,
∴BD=$\sqrt{5}$AT,DT=$\frac{2\sqrt{5}}{5}$CD.
∵CD=70m,
∴DT=70×$\frac{2\sqrt{5}}{5}=28\sqrt{5}$(m).
∵∠ADT=∠ADC + ∠CDT=∠ADC + ∠ABC=90°,
∴AT=$\sqrt{AD^2 + DT^2}=4\sqrt{870}$m,
∴BD=$\sqrt{5}$AT=20$\sqrt{174}$m.