《2025年5年中考3年模拟九年级数学上册沪科版》

1.跨物理电学「2025安徽淮北二中期中」已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系$(I= \frac {U}{R})$.下列反映电流I与电阻R之间函数关系的图象大致是( )

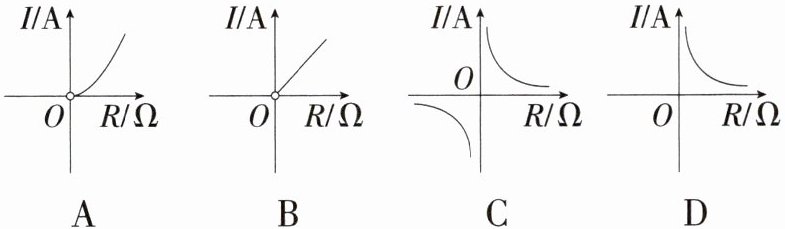
答案： D
∵电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系$(I=\frac {U}{R})$,R,I均大于0,
∴反映电流I与电阻R之间函数关系的图象大致是D选项中的图象.故选D.

2.「2025安徽六安皋城中学月考」验光师检测发现近视眼镜的度数y(度)与镜片焦距x(米)成反比例关系,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了( )


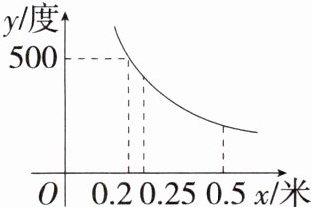
A.150度
B.200度
C.250度
D.300度

答案： B 设y与x之间的函数表达式为$y=\frac {k}{x}(k≠0),$
∵点$(0.2,500)$在图象上,$\therefore k=500×0.2=100$,
∴y与x之间的函数表达式为$y=\frac {100}{x}$.当$x=0.25$时,$y=\frac {100}{0.25}=$400;当$x=0.5$时,$y=\frac {100}{0.5}=200$,
∴近视眼镜的度数减少了$400-200=200$(度).故选B.

3.跨物理杠杆原理「2024江苏连云港中考」杠杆平衡时,“阻力×阻力臂= 动力×动力臂”.已知阻力和阻力臂分别为1600N和0.5m,动力为F(N),动力臂为l(m),则动力F关于动力臂l的函数表达式为______.

答案： 答案$F=\frac {800}{l}$
解析 由题意得$l\cdot F=1600×0.5,\therefore F=\frac {800}{l}.$

4. 1896年,挪威生理学家古德贝发现,每个人一只脚迈出的步子比另一只脚迈出的步子长,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈,这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y(米)是其两脚迈出的步长之差x(厘米)$(x＞0)$的反比例函数,其图象如图所示.若此人蒙上眼睛走出的大圆圈的半径不小于35米,则其两脚迈出的步长之差最多是______厘米.

答案： 答案 0.4
解析 设y与x之间的函数表达式为$y=\frac {k}{x}(k≠0),$
∵图象过$(2,7),\therefore 7=\frac {k}{2},\therefore k=14$,
∴y与x之间的函数表达式为$y=\frac {14}{x}$.当$y≥35$,即$\frac {14}{x}≥35$时,解得$x≤$0.4,
∴两脚迈出的步长之差最多是0.4厘米.

5.学科教材变式特色P44例1跨物理压强某气球内充满了一定质量的气体,当温度不变时,气球内的气压p(千帕)是气体体积V(立方米)的反比例函数,其图象如图所示.(千帕是一种压强单位)
(1)求该反比例函数的表达式.
(2)当气体体积为3立方米时,气球内的气压是多少千帕?
(3)当气球内的气压为120千帕时,求气体体积.

答案： 解析
(1)设$p=\frac {k}{V}(V＞0).$将$(2,48)$代入$p=\frac {k}{V}(V＞0)$,得$48=\frac {k}{2},$解得$k=96,$
∴该反比例函数的表达式为$p=\frac {96}{V}(V＞0).$
(2)当$V=3$(立方米)时,$p=\frac {96}{3}=32$(千帕),答:当气体体积为3立方米时,气球内的气压是32千帕.
(3)当$p=120$(千帕)时,$V=\frac {96}{120}=0.8$(立方米).答:当气球内的气压为120千帕时,气体体积为0.8立方米.