《2025年5年中考3年模拟九年级数学上册沪科版》

6.「2024 新疆生产建设兵团中考,」某公司销售一批产品,经市场调研发现,当销售量在 0.4 吨至 3.5 吨之间时,销售额 $y_{1}$(万元)与销售量 x(吨)的函数表达式为 $y_{1}= 5x$；成本 $y_{2}$(万元)与销售量 x(吨)的函数图象是如图所示的抛物线的一部分,其中点 $(\frac{1}{2},\frac{7}{4})$ 是其顶点。
(1)求出成本 $y_{2}$ 关于销售量 x 的函数表达式。
(2)当成本最低时,销售产品所获利润是多少？
(3)当销售量是多少吨时,可获得最大利润？最大利润是多少？(注：利润= 销售额-成本)

答案：
(1)
∵抛物线顶点为(1/2,7/4),
∴可设抛物线表达式为y₂=a(x-1/2)²+7/4.
∵抛物线过点(2,4),
∴a×9/4+7/4=4,解得a=1.
∴y₂=(x-1/2)²+7/4.
(2)由
(1)知,y₂=(x-1/2)²+7/4,
∵1＞0,
∴x=1/2时,y₂取得最小值,即当x=1/2时,成本最低,最低成本为7/4万元,
∵销售量在0.4吨至3.5吨之间时,销售额y₁(万元)与销售量x(吨)的函数表达式为y₁=5x,
∴当x=1/2时,y₁=5×1/2=2.5. 此时利润为2.5-7/4=0.75(万元). 答:当成本最低时,销售产品所获利润是0.75万元.
(3)由题意,得利润=y₁-y₂=5x-[(x-1/2)²+7/4]=-x²+6x-2=-(x-3)²+7.
∵-1＜0,
∴当x=3时,利润取得最大值,最大值为7. 答:当销售量是3吨时,可获得最大利润,最大利润是7万元.

7.新应用意识「2022 浙江金华中考」“八婺”菜场指导菜农生产和销售某种蔬菜,提供如下信息：
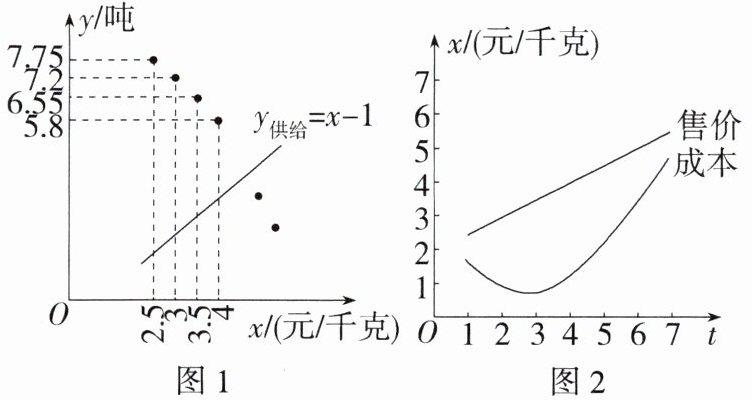
①统计售价与需求量的数据,通过描点(图 1),发现该蔬菜需求量 $y_{需求}$(吨)关于售价 x(元/千克)的函数图象可以看成抛物线,其表达式为 $y_{需求}= ax^{2}+c$,部分对应值如下表：
|售价 x/(元/千克)|…|2.5|3|3.5|4|…|
|需求量 $y_{需求}$/吨|…|7.75|7.2|6.55|5.8|…|

②该蔬菜供给量 $y_{供给}$(吨)关于售价 x(元/千克)的函数表达式为 $y_{供给}= x-1$,函数图象见图 1。
③1~7 月份该蔬菜售价 $x_{售价}$(元/千克)、成本 $x_{成本}$(元/千克)关于月份 t 的函数表达式分别为 $x_{售价}= \frac{1}{2}t+2$,$x_{成本}= \frac{1}{4}t^{2}-\frac{3}{2}t+3$,函数图象见图 2。

请解答下列问题：
(1)求 a,c 的值。
(2)根据图 2,判断哪个月出售这种蔬菜每千克获利最大,并说明理由。
(3)求该蔬菜供给量与需求量相等时的售价,以及按此价格出售获得的总利润。

答案：
(1)把(3,7.2),(4,5.8)代入y_需求=ax²+c, 得{9a+c=7.2,16a+c=5.8,解得{a=-1/5,c=9.
(2)设这种蔬菜每千克获利w元,根据题意得 w=x_售价-x_成本=1/2t+2-(1/4t²-3/2t+3)=-1/4(t-4)²+3,
∵-1/4＜0,且1≤t≤7,
∴当t=4时,w有最大值, 故在4月份出售这种蔬菜每千克获利最大.
(3)由
(1)可知y_需求=-1/5x²+9,当y_供给=y_需求时,x-1=-1/5x²+9,解得x₁=5,x₂=-10(舍去),
∴供给量为5-1=4吨=4000千克,令1/2t+2=5,解得t=6,
∴每千克获利=-1/4×(6-4)²+3=2(元),
∴总利润为2×4000=8000(元).答:该蔬菜供给量与需求量相等时的售价为5元/千克,按此价格出售获得的总利润为8000元.