《2025年5年中考3年模拟九年级数学上册沪科版》

1.下列条件中,一定能判定两个等腰三角形相似的是 ( )

A.都含有一个$40^{\circ }$的内角
B.都含有一个$50^{\circ }$的内角
C.都含有一个$60^{\circ }$的内角
D.都含有一个$70^{\circ }$的内角

答案： C　若等腰三角形中有一个角是60°,则这个三角形是等边三角形，两个等边三角形一定相似，故选C.

2.「2024安徽淮北月考」如图,$△ABC$中,点D在AB边上,点E在AC边上,且$∠1= ∠2= ∠3$,则与$△ADE$相似的三角形的个数为 ( )

A.4
B.3
C.2
D.1

答案： C
∵∠1=∠2,∠A=∠A,
∴△ADE∽△ABC,
∵∠1=∠3,∠A=∠A,
∴△ADE∽△ACD,
∴题图中与△ADE 相似的三角形有2个.故选C.

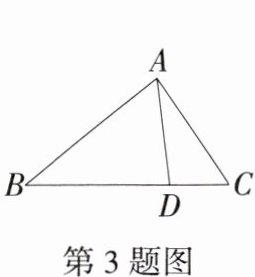
3.学科母子型特色相似如图,若$∠B= ∠DAC$,则$△ABC\backsim △$____.

答案： 答案　DAC
解析　在△ABC和△DAC中,因为∠C=∠C,∠B=∠DAC,所以△ABC∽△DAC.

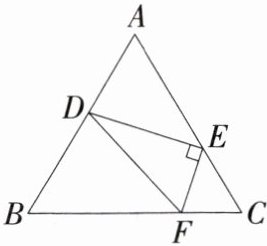
4.学科一线三等特色角型相似「2025安徽合肥五十中西校期中」如图,点D,E,F分别在等边$△ABC$的三边AB,AC,BC上,且$DE⊥EF,∠DFE= 60^{\circ }$.
(1)求证:$△DBF\backsim △FCE.$
(2)若$CE= 1$,求BF的长.

答案： 解析　
(1)证明:
∵△ABC为等边三角形，
∴∠B=∠C=60°,
∴∠BDF+∠DFB=180°−60°=120°.
∵∠DFE=60°,
∴∠DFB+∠EFC=180°−60°=120°,
∴∠BDF=∠EFC,
∴△DBF∽△FCE.
(2)
∵DE⊥EF,∠DFE=60°,
∴∠EDF=30°,
∴DF=2EF.由
(1)知,△DBF∽△FCE,
∴$\frac{BF}{CE}$=$\frac{DF}{EF}$=2.
∵CE=1,
∴BF=2.

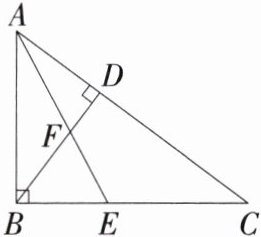
5.「2024山东德州中考,」如图,在$Rt△ABC$中,$∠ABC= 90^{\circ },BD⊥AC$,垂足为D,AE平分$∠BAC$,分别交BD,BC于点F,E.若$AB:BC= 3:4$,则$BF:FD= $ ( )


A.$5:3$
B.$5:4$
C.$4:3$
D.$2:1$

答案： A
∵AB∶BC=3∶4,
∴设AB=3x,则BC=4x.
∵∠ABC=90°,
∴AC=√(AB²+BC²)=5x.
∵BD⊥AC,
∴∠ADB=∠ABC=90°.
∵∠BAD=∠CAB,
∴△ABD∽△ACB,
∴$\frac{AB}{AC}$=$\frac{AD}{AB}$,
∴$\frac{3x}{5x}$=$\frac{AD}{3x}$,
∴AD=$\frac{9}{5}$x.
∵AE平分∠BAC,
∴∠BAF=∠DAF,
∴∠AEB=∠AFD.
∵∠AFD =∠BFE,
∴∠BEF=∠BFE,
∴BE=BF.
∵∠ABE=∠ADF=90°,∠BAE=∠DAF,
∴△ABE∽△ADF,
∴$\frac{BE}{DF}$=$\frac{AB}{AD}$,
∴$\frac{BF}{DF}$=$\frac{AB}{AD}$=$\frac{3x}{\frac{9}{5}x}$=$\frac{5}{3}$,即BF∶FD=5∶3.故选A.

6.「2025安徽合肥四十二中期中,」如图,在$△ABC$中,$∠ACB= 90^{\circ }$,点P为$△ABC内部一点且始终满足∠ACP= ∠CBP$,延长BP交AC于点D.
(1)求证:$CD^{2}= DP\cdot DB.$
(2)若$∠APB= 90^{\circ }+∠CBA$,求证:$AD= CD.$

答案： 证明　
(1)
∵∠ACP=∠CBP,∠CDP=∠CDB,
∴△CDP∽△BDC,
∴$\frac{CD}{BD}$=$\frac{DP}{CD}$,
∴CD²=DP·DB.
(2)
∵∠APB=90°+∠CBA,
∴∠APD=180°-(90°+∠CBA)=90°-∠CBA,
∵∠ACB=90°,
∴∠CAB=90°-∠CBA,
∴∠APD=∠DAB.
∵∠ADP=∠ADB,
∴△ADP∽△BDA,
∴$\frac{AD}{DB}$=$\frac{DP}{AD}$,
∴AD²=DP·DB.
∵CD²=DP·DB,
∴AD=CD.

7.新课标推理能力学科分类讨特色论思想如图,在$Rt△ABC$中,$∠C= 90^{\circ },AC= 4,BC= 3$,P是斜边AB上的一点,且$AP= 2$.过点P作一条直线,与$Rt△ABC$另一边的交点为D,并且截得的三角形与$Rt△ABC$相似,则PD的长为____.

答案： 答案　$\frac{6}{5}$或$\frac{12}{5}$或$\frac{3}{2}$
解析　分三种情况讨论:如图1,过点P作PD⊥AC于点D,则∠ADP=∠C=90°.又
∵∠DAP=∠CAB,
∴△ADP∽△ACB,
∴$\frac{PD}{BC}$=$\frac{AP}{AB}$,
∵AB=√(AC²+BC²)=√(4²+3²)=5,
∴$\frac{PD}{3}$=$\frac{2}{5}$,解得PD=$\frac{6}{5}$.
如图2,过点P作PD⊥BC于点D,则∠PDB=∠C=90°.又
∵∠PBD=∠ABC,
∴△PBD∽△ABC,
∴$\frac{PD}{AC}$=$\frac{PB}{AB}$,即$\frac{PD}{4}$=$\frac{5−2}{5}$,解得PD=$\frac{12}{5}$.
如图3,过点P作PD⊥AB,交AC于点D,则∠APD=∠ACB=90°.
∵∠DAP=∠BAC,
∴△ADP∽△ABC,
∴$\frac{PD}{BC}$=$\frac{AP}{AC}$,即$\frac{PD}{3}$=$\frac{2}{4}$,解得PD=$\frac{3}{2}$.
综上,PD的长为$\frac{6}{5}$或$\frac{12}{5}$或$\frac{3}{2}$.