第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
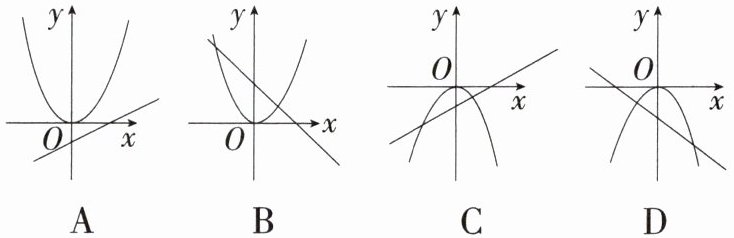
11.「2025 安徽安庆外国语学校月考,」当$ab>0$时,$y= ax^{2}与y= ax+b$的图象大致是( )
A
B
C
D

A
B
C
D
答案:
D ab>0,即a,b同号。当a>0,b>0时,y=ax²的图象开口向上,经过原点,y=ax+b的图象过第一、二、三象限,此时没有选项符合。当a<0,b<0时,y=ax²的图象开口向下,经过原点,y=ax+b的图象过第二、三、四象限,此时D选项符合。故选D。
12.「2024 安徽宣城期末,」已知点$A(1,1),B(3,1),C(3,2),D(1,2)$,若抛物线$y= ax^{2}(a>0)与四边形ABCD$的边没有交点,则$a$的取值范围为( )
A.$\frac {1}{9}<a<1$
B.$\frac {2}{9}<a<1$
C.$a>2或0<a<\frac {1}{9}$
D.$a>1或0<a<\frac {2}{9}$
A.$\frac {1}{9}<a<1$
B.$\frac {2}{9}<a<1$
C.$a>2或0<a<\frac {1}{9}$
D.$a>1或0<a<\frac {2}{9}$
答案:
C 如图所示,把D(1,2)代入y=ax²(a>0),得a=2。把B(3,1)代入y=ax²得a=$\frac{1}{9}$。
∵ 抛物线的开口越小,|a|越大,
∴ 当抛物线y=ax²(a>0)与四边形ABCD的边没有交点时,a的取值范围为a>2或0<a<$\frac{1}{9}$。故选C。

C 如图所示,把D(1,2)代入y=ax²(a>0),得a=2。把B(3,1)代入y=ax²得a=$\frac{1}{9}$。
∵ 抛物线的开口越小,|a|越大,
∴ 当抛物线y=ax²(a>0)与四边形ABCD的边没有交点时,a的取值范围为a>2或0<a<$\frac{1}{9}$。故选C。

13.「2025 北京西城育才学校月考,」对于二次函数$y= ax^{2}和y= bx^{2}$,其自变量和函数值的两组对应值如表所示:
| $x$ | $-1$ | $m(m≠-1)$ |
| $y= ax^{2}$ | $c$ | $c$ |
| $y= bx^{2}$ | $c+3$ | $d$ |
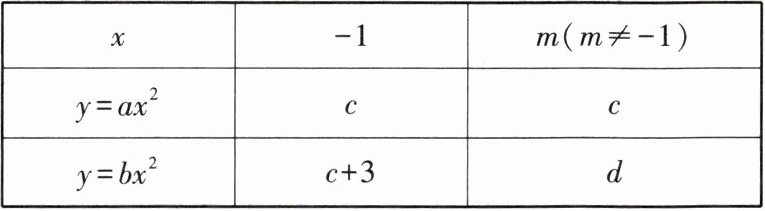
根据二次函数图象的相关性质可知:$m= $____,$d-c= $____.
| $x$ | $-1$ | $m(m≠-1)$ |
| $y= ax^{2}$ | $c$ | $c$ |
| $y= bx^{2}$ | $c+3$ | $d$ |

根据二次函数图象的相关性质可知:$m= $____,$d-c= $____.
答案:
答案 1;3
解析 抛物线y=ax²和y=bx²的对称轴都为y轴,可将题表中的数表示为坐标(−1,c),(m,c),(−1,c+3),(m,d)。
∵ (−1,c),(m,c)两点纵坐标相等,且m ≠−1,
∴ m=1。
∵ (−1,c+3),(m,d)两点的横坐标关于y轴对称,
∴ d=c+3,
∴ d−c=3。
解析 抛物线y=ax²和y=bx²的对称轴都为y轴,可将题表中的数表示为坐标(−1,c),(m,c),(−1,c+3),(m,d)。
∵ (−1,c),(m,c)两点纵坐标相等,且m ≠−1,
∴ m=1。
∵ (−1,c+3),(m,d)两点的横坐标关于y轴对称,
∴ d=c+3,
∴ d−c=3。
14.「2024 广西南宁天桃实验学校月考,」已知点$A(2,4),B(0,1)$,点$M在抛物线y= \frac {1}{4}x^{2}$上运动,则$AM+BM$的最小值为____.
答案:
答案 5
解析 设点M(m,$\frac{1}{4}$m²),则点M到x轴的距离为$\frac{1}{4}$m²,BM=$\sqrt{(m−0)²+(\frac{1}{4}m²−1)²}$=$\frac{1}{4}$m²+1,
∴ 点M到点B的距离与点M到直线y=−1的距离相等。
∵ 点A的横坐标为2,
∴ 点M为直线x=2与抛物线的交点时,AM+BM取得最小值。如图,设直线x=2与直线y=−1的交点为B',则B'(2,−1),
∴ AB'的长为AM+BM的最小值,AB'=4−(−1)=5。故答案为5。

答案 5
解析 设点M(m,$\frac{1}{4}$m²),则点M到x轴的距离为$\frac{1}{4}$m²,BM=$\sqrt{(m−0)²+(\frac{1}{4}m²−1)²}$=$\frac{1}{4}$m²+1,
∴ 点M到点B的距离与点M到直线y=−1的距离相等。
∵ 点A的横坐标为2,
∴ 点M为直线x=2与抛物线的交点时,AM+BM取得最小值。如图,设直线x=2与直线y=−1的交点为B',则B'(2,−1),
∴ AB'的长为AM+BM的最小值,AB'=4−(−1)=5。故答案为5。

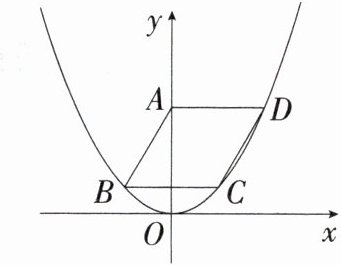
15.「2023 江苏扬州中考节选,」在平面直角坐标系$xOy$中,已知点$A在y$轴正半轴上.如果四个点$(0,0),(0,2),(1,1),(-1,1)中恰有三个点在二次函数y= ax^{2}$($a$为常数,且$a≠0$)的图象上.
(1)$a= $____.
(2)如图,已知菱形$ABCD的顶点B,C,D$在该二次函数的图象上,且$AD⊥y$轴,求菱形的边长.
(1)$a= $____.
(2)如图,已知菱形$ABCD的顶点B,C,D$在该二次函数的图象上,且$AD⊥y$轴,求菱形的边长.

答案:
解析
(1)1。
详解:在y=ax²中,令x=0得y=0,
∴ (0,0)在二次函数y=ax²(a为常数,且a≠0)的图象上,(0,2)不在二次函数y=ax²(a为常数,且a≠0)的图象上。
∵ 四个点(0,0),(0,2),(1,1),(−1,1)中恰有三个点在二次函数y=ax²(a为常数,且a≠0)的图象上,
∴ (0,0),(1,1),(−1,1)这三个点在二次函数y=ax²(a为常数,且a≠0)的图象上。把(1,1)代入y=ax²,得a=1。
(2)设BC交y轴于E,如图。设菱形的边长为2t,则AB=BC=CD=AD=2t。易知B,C关于y轴对称,
∴ BE =CE=t,
∴ B(−t,t²),
∴ OE=t²。
∵ AE=$\sqrt{AB²−BE²}$=$\sqrt{3}$t,
∴ OA=OE+AE=t²+$\sqrt{3}$t,
∴ D(2t,t²+$\sqrt{3}$t)。把D(2t,t²+$\sqrt{3}$t)代入y=x²,得t²+$\sqrt{3}$t=4t²,解得t=$\frac{\sqrt{3}}{3}$或t=0(舍去),
∴ 菱形的边长为$\frac{2\sqrt{3}}{3}$。

解析
(1)1。
详解:在y=ax²中,令x=0得y=0,
∴ (0,0)在二次函数y=ax²(a为常数,且a≠0)的图象上,(0,2)不在二次函数y=ax²(a为常数,且a≠0)的图象上。
∵ 四个点(0,0),(0,2),(1,1),(−1,1)中恰有三个点在二次函数y=ax²(a为常数,且a≠0)的图象上,
∴ (0,0),(1,1),(−1,1)这三个点在二次函数y=ax²(a为常数,且a≠0)的图象上。把(1,1)代入y=ax²,得a=1。
(2)设BC交y轴于E,如图。设菱形的边长为2t,则AB=BC=CD=AD=2t。易知B,C关于y轴对称,
∴ BE =CE=t,
∴ B(−t,t²),
∴ OE=t²。
∵ AE=$\sqrt{AB²−BE²}$=$\sqrt{3}$t,
∴ OA=OE+AE=t²+$\sqrt{3}$t,
∴ D(2t,t²+$\sqrt{3}$t)。把D(2t,t²+$\sqrt{3}$t)代入y=x²,得t²+$\sqrt{3}$t=4t²,解得t=$\frac{\sqrt{3}}{3}$或t=0(舍去),
∴ 菱形的边长为$\frac{2\sqrt{3}}{3}$。

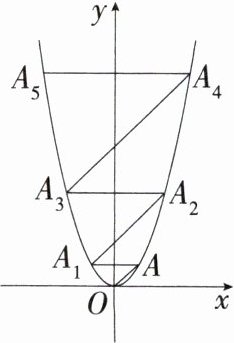
16. 几何直观 规律探究题「2025 广西钦州一中期中」在平面直角坐标系中,抛物线$y= x^{2}$如图所示,已知点$A的坐标为(1,1)$,过点$A作AA_{1}// x轴交抛物线于点A_{1}$,过点$A_{1}作A_{1}A_{2}// OA交抛物线于点A_{2}$,过点$A_{2}作A_{2}A_{3}// x轴交抛物线于点A_{3}$,过点$A_{3}作A_{3}A_{4}// OA交抛物线于点A_{4}$,……,依次进行下去,则点$A_{2024}$的坐标为____.

答案:
答案 (1013,1013²)
解析
∵ 点A的坐标为(1,1),
∴ 直线OA的表达式为y₁=x。
∵ AA₁//x轴,且点A₁在抛物线y=x²上,
∴ 点A₁的坐标为(−1,1)。
∵ A₁A₂//OA,
∴ 直线A₁A₂的表达式为y₂=x+2。将直线A₁A₂的表达式与抛物线的表达式联立,得$\begin{cases}y = x + 2\\y = x^{2}\end{cases}$,解得$\begin{cases}x = -1\\y = 1\end{cases}$或$\begin{cases}x = 2\\y = 4\end{cases}$,
∴ 点A₂的坐标为(2,4)。
∵ A₂A₃//x轴,且点A₃在抛物线上,
∴ 点A₃的坐标为(−2,4)。同理可求得点A₄的坐标为(3,9),点A₅的坐标为(−3,9),……,依此规律,点A₂ₙ的坐标为(n + 1,(n + 1)²),
∴ 点A₂₀₂₄的坐标为(1013,1013²)。
解析
∵ 点A的坐标为(1,1),
∴ 直线OA的表达式为y₁=x。
∵ AA₁//x轴,且点A₁在抛物线y=x²上,
∴ 点A₁的坐标为(−1,1)。
∵ A₁A₂//OA,
∴ 直线A₁A₂的表达式为y₂=x+2。将直线A₁A₂的表达式与抛物线的表达式联立,得$\begin{cases}y = x + 2\\y = x^{2}\end{cases}$,解得$\begin{cases}x = -1\\y = 1\end{cases}$或$\begin{cases}x = 2\\y = 4\end{cases}$,
∴ 点A₂的坐标为(2,4)。
∵ A₂A₃//x轴,且点A₃在抛物线上,
∴ 点A₃的坐标为(−2,4)。同理可求得点A₄的坐标为(3,9),点A₅的坐标为(−3,9),……,依此规律,点A₂ₙ的坐标为(n + 1,(n + 1)²),
∴ 点A₂₀₂₄的坐标为(1013,1013²)。
查看更多完整答案,请扫码查看


