《2025年5年中考3年模拟九年级数学上册沪科版》

1. 学科教材变式 [2025上海宝山一模]在$Rt△ABC$中,$∠C= $ $90^{\circ },sinA= \frac {1}{2}$,那么$cosB$的值是 ( )

A.$\frac {\sqrt {3}}{2}$
B.$\frac {1}{2}$
C.$\frac {\sqrt {3}}{3}$
D.$\sqrt {3}$

答案： B

2. 若$sin(70^{\circ }-α)= cos50^{\circ }$,则α的度数是 ( )

A.$50^{\circ }$
B.$40^{\circ }$
C.$30^{\circ }$
D.$20^{\circ }$

答案： C

3. $∠A,∠B,∠C是△ABC$的三个内角,则$sin\frac {A+B}{2}= $ ( )

A.$cos\frac {C}{2}$
B.$sin\frac {C}{2}$
C.$cosC$
D.$cos\frac {A+B}{2}$

答案： A

4. [2025安徽亳州月考]比较大小:$sin47^{\circ }$____$cos43^{\circ }$.

答案： =

5. 如图,在$Rt△ABC$中,$∠C= 90^{\circ },a,b,c分别表示Rt△ABC中∠A,∠B,∠C$的对边.
(1) 求$sinA,cosB$.
(2) 求$tanA,tanB,tanA\cdot tanB$.
(3) 观察(1)(2)中的计算结果,若$α+β= 90^{\circ }$,试猜想$sinα与cosβ,tanα与tanβ$之间有什么关系.

(4) 应用:
①在$Rt△ABC$中,$∠C= 90^{\circ },sinA= \frac {2}{3}$,则$cosB$的值为____;
②在$Rt△ABC$中,$∠C= 90^{\circ },tanA= 2$,则$tanB= $____.

答案：
(1)在Rt△ABC中,∠C=90°,sinA=$\frac{a}{c}$,cosB=$\frac{a}{c}$.
(2)在Rt△ABC中,∠C=90°,tanA=$\frac{a}{b}$,tanB=$\frac{b}{a}$,tanA·tanB=$\frac{a}{b}$·$\frac{b}{a}$=1.
(3)当α+β=90°时,由
(1)知sinα=cosβ,由
(2)知tanα·tanβ=1.
(4)①$\frac{2}{3}$
②$\frac{1}{2}$

6. [2025山东聊城慧德学校月考]比较$tan52^{\circ },$ $cos21^{\circ },sin49^{\circ }$的大小关系是 ( )

A.$tan52^{\circ }＜cos21^{\circ }＜sin49^{\circ }$
B.$tan52^{\circ }＜sin49^{\circ }＜cos21^{\circ }$
C.$sin49^{\circ }＜tan52^{\circ }＜cos21^{\circ }$
D.$sin49^{\circ }＜cos21^{\circ }＜tan52^{\circ }$

答案： D

7. [2024河南安阳滑县期末]如图,根据图中数据完成填空,再按要求答题.

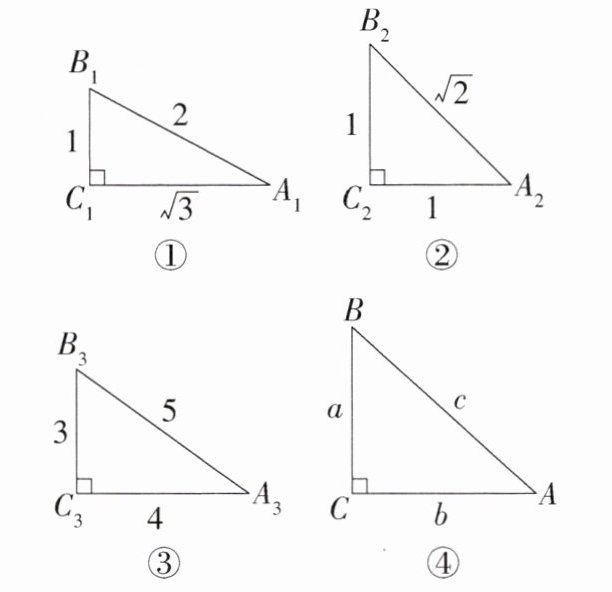
$sin^{2}A_{1}+sin^{2}B_{1}= $____;$sin^{2}A_{2}+sin^{2}B_{2}= $____; $sin^{2}A_{3}+sin^{2}B_{3}= $____.
(1) 观察上述等式,猜想:在$Rt△ABC$中,若$∠C= 90^{\circ }$,则$sin^{2}A+sin^{2}B= $____.
(2) 如图④,在$Rt△ABC$中,$∠C= 90^{\circ },∠A,$ $∠B,∠C的对边分别是a,b,c$,利用三角函数的定义和勾股定理,证明你的猜想.
(3) 已知$∠A+∠B= 90^{\circ }$,且$sinA= \frac {5}{13}$,求$sinB$的值.

答案： 1;1;1
(1)1
(2)在Rt△ABC中,∠C=90°,
∴sinA=$\frac{a}{c}$,sinB=$\frac{b}{c}$,
∴sin²A+sin²B=$\frac{a²+b²}{c²}$,
∵a²+b²=c²,
∴sin²A+sin²B=1.
(3)$\frac{12}{13}$