《2025年5年中考3年模拟九年级数学上册沪科版》

8.「2025安徽六安皋城中学期中,★☆」如图,△ABC与△DEF位似,点O是位似中心,若OA：AD= 1：2,DF-AC= 8,则DF+AC= ( )

A.8
B.12
C.16
D.18

答案： C
∵△ABC与△DEF位似,点O是位似中心,OA:AD=1:2,
∴AC//DF,$\frac{OA}{OD}=\frac{1}{3}$,
∴△OAC∽△ODF,
∴$\frac{AC}{DF}=\frac{OA}{OD}=\frac{1}{3}$,
∴DF=3AC,
∵DF - AC = 8,
∴3AC - AC = 2AC = 8,解得AC = 4,
∴DF = 3AC = 12,
∴DF + AC = 12 + 4 = 16.故选C.

9.新考向规律探究题「2022山东威海中考,★☆」由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB= ∠BOC= ∠COD=… =∠LOM= 30°.若S△AOB= 1,则图中与△AOB位似的三角形的面积为( )


A.$(\frac{4}{3})^{3}$
B.$(\frac{4}{3})^{7}$
C.$(\frac{4}{3})^{6}$
D.$(\frac{3}{4})^{6}$

答案： C　在Rt△AOB中,∠AOB = 30°,设AB = a,则OB = 2a,
∴OA = $\sqrt{3}$a,
∴OB = $\frac{2}{\sqrt{3}}$OA,同理,OC = $\frac{2}{\sqrt{3}}$OB,
∴OC = $(\frac{2}{\sqrt{3}})^2$OA,……,OG = $(\frac{2}{\sqrt{3}})^6$OA,由位似图形的定义可知,△GOH与△AOB位似,且相似比为$(\frac{2}{\sqrt{3}})^6$:1,
∵S△AOB = 1,
∴S△GOH = $[(\frac{2}{\sqrt{3}})^6]^2 = (\frac{4}{3})^6$,故选C.

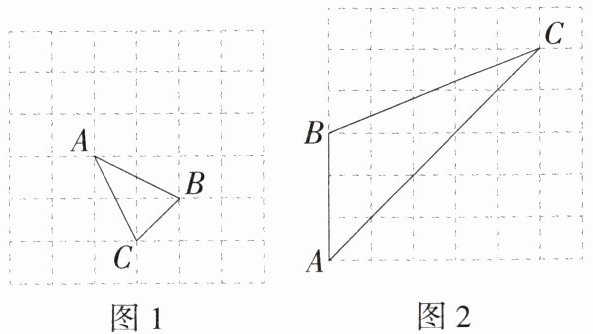
10.「2025安徽安庆外国语学校期末,★☆」如图,在正方形网格中,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,利用格点按要求完成下列作图.(要求仅用无刻度的直尺,不要求写画法,保留必要的作图痕迹)
(1)在图1中,以C为位似中心作$△A_1B_1C_1,$使它与△ABC的相似比为2：1.
(2)在图2中,在AC边上找一点E,使△ADE∽△ABC.

答案：
解析　
(1)如图,△A₁B₁C即为所求
　　　　　　　　
(2)如图，点E即为所求.(答案不唯一)
　　　　　　　

11.新考向规律探究题新课标创新意识如图所示的是由位似的正$△A_1B_1C_1,$正$△A_2B_2C_2,$正$△A_3B_3C_3,…,$正△AₙBₙCₙ组成的图形,其中$△A_1B_1C_1$的边长为1,点O是$B_1C_1$的中点$,A_2$是$OA_1$的中点$,A_3$是$OA_2$的中点,……,Aₙ是$OAₙ₋_1$的中点,顶点$B_2,B_3,…,Bₙ$和顶点$C_2,C_3,…,Cₙ$都在$B_1C_1$边上.
(1)试写出$△A_1₀B_1₀C_1₀$和$△A_7B_7C_7$的相似比和位似中心.
(2)求出△AₙBₙCₙ(n≥2)的周长.

答案： 解析　
(1)
∵△A₁B₁C₁的边长为1,点O是B₁C₁的中点,A₂是OA₁的中点,
∴正△A₂B₂C₂的边长为$\frac{1}{2}$,正△A₃B₃C₃的边长为$(\frac{1}{2})^2$,……正△A₇B₇C₇的边长为$(\frac{1}{2})^6$,正△A₁₀B₁₀C₁₀的边长为$(\frac{1}{2})^9$,
∴正△A₁₀B₁₀C₁₀和正△A₇B₇C₇的相似比 = $\frac{(\frac{1}{2})^9}{(\frac{1}{2})^6}=\frac{1}{8}$.它们的位似中心为点O.
(2)
∵△AₙBₙCₙ(n≥2)的边长为$(\frac{1}{2})^{n - 1}$,
∴△AₙBₙCₙ(n≥2)的周长为$\frac{3}{2^{n - 1}}$.