第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
6.跨物理上抛运动「2024天津中考,★☆」从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是$h= 30t-5t^{2}(0≤t≤6)$.下列结论:
①小球从抛出到落地需要6s;
②小球运动中的高度可以是30m;
③小球运动2s时的高度小于运动5s时的高度.
其中,正确结论的个数是( )
A.0
B.1
C.2
D.3
①小球从抛出到落地需要6s;
②小球运动中的高度可以是30m;
③小球运动2s时的高度小于运动5s时的高度.
其中,正确结论的个数是( )
A.0
B.1
C.2
D.3
答案:
C ①令h=0,则$30t-5t^{2}=0$,解得$t_{1}=0,t_{2}=6$,
∴小球从抛出到落地需要6s,故①正确;②$h=30t-5t^{2}=-5(t^{2}-6t)=-5(t-3)^{2}+45$,
∵$-5<0$,
∴当t=3时,h有最大值,为45,
∴小球运动中的高度可以是30m,故②正确;③t=2时,$h=30×2-5×4=40$;t=5时,$h=30×5-5×25=25$,
∵40>25,
∴小球运动2s时的高度大于运动5s时的高度,故③错误.故选C.
∴小球从抛出到落地需要6s,故①正确;②$h=30t-5t^{2}=-5(t^{2}-6t)=-5(t-3)^{2}+45$,
∵$-5<0$,
∴当t=3时,h有最大值,为45,
∴小球运动中的高度可以是30m,故②正确;③t=2时,$h=30×2-5×4=40$;t=5时,$h=30×5-5×25=25$,
∵40>25,
∴小球运动2s时的高度大于运动5s时的高度,故③错误.故选C.
7.「2023河北中考,★☆」嘉嘉和淇淇在玩扔沙包游戏.某同学借此情境编了一道数学题,请解答这道题.
如图,在平面直角坐标系中,一个单位长度代表1m长.嘉嘉在点$A(6,1)$处将沙包(看成点)抛出,其运动路线为抛物线$C_{1}:y= a(x-3)^{2}+2$的一部分,淇淇恰在点$B(0,c)$处接住,然后跳起将沙包回传,其运动路线为抛物线$C_{2}:y= -\frac {1}{8}x^{2}+\frac {n}{8}x+c+1$的一部分.
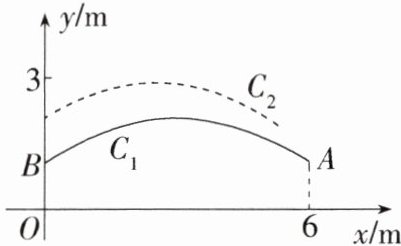
(1)写出抛物线$C_{1}$的最高点的坐标,并求a,c的值.
(2)若嘉嘉在x轴上方1m的高度上,且到点A水平距离不超过1m的范围内可以接到沙包,求符合条件的n的整数值.
如图,在平面直角坐标系中,一个单位长度代表1m长.嘉嘉在点$A(6,1)$处将沙包(看成点)抛出,其运动路线为抛物线$C_{1}:y= a(x-3)^{2}+2$的一部分,淇淇恰在点$B(0,c)$处接住,然后跳起将沙包回传,其运动路线为抛物线$C_{2}:y= -\frac {1}{8}x^{2}+\frac {n}{8}x+c+1$的一部分.

(1)写出抛物线$C_{1}$的最高点的坐标,并求a,c的值.
(2)若嘉嘉在x轴上方1m的高度上,且到点A水平距离不超过1m的范围内可以接到沙包,求符合条件的n的整数值.
答案:
(1)
∵抛物线$C_{1}:y=a(x-3)^{2}+2$,
∴抛物线$C_{1}$的最高点的坐标为(3,2).
∵点A(6,1)在抛物线$C_{1}:y=a(x-3)^{2}+2$上,
∴$1=a(6-3)^{2}+2$,
∴$a=-\frac {1}{9}$.
∴抛物线$C_{1}:y=-\frac {1}{9}(x-3)^{2}+2$,当x=0时,y=c=1.
(2)设嘉嘉的位置为点D.
∵嘉嘉在x轴上方1m的高度上,且到点A水平距离不超过1m的范围内可以接到沙包,
∴点D的横坐标的取值范围是$5≤x_{D}≤7$,当抛物线$C_{2}$经过(5,1)时,$1=-\frac {1}{8}×25+\frac {n}{8}×5+1+1$,解得$n=\frac {17}{5}$,当抛物线$C_{2}$经过(7,1)时,$1=-\frac {1}{8}×49+\frac {n}{8}×7+1+1$,解得$n=\frac {41}{7}$,
∴$\frac {17}{5}≤n≤\frac {41}{7}$,
∵n为整数,
∴符合条件的n的整数值为4和5.
(1)
∵抛物线$C_{1}:y=a(x-3)^{2}+2$,
∴抛物线$C_{1}$的最高点的坐标为(3,2).
∵点A(6,1)在抛物线$C_{1}:y=a(x-3)^{2}+2$上,
∴$1=a(6-3)^{2}+2$,
∴$a=-\frac {1}{9}$.
∴抛物线$C_{1}:y=-\frac {1}{9}(x-3)^{2}+2$,当x=0时,y=c=1.
(2)设嘉嘉的位置为点D.
∵嘉嘉在x轴上方1m的高度上,且到点A水平距离不超过1m的范围内可以接到沙包,
∴点D的横坐标的取值范围是$5≤x_{D}≤7$,当抛物线$C_{2}$经过(5,1)时,$1=-\frac {1}{8}×25+\frac {n}{8}×5+1+1$,解得$n=\frac {17}{5}$,当抛物线$C_{2}$经过(7,1)时,$1=-\frac {1}{8}×49+\frac {n}{8}×7+1+1$,解得$n=\frac {41}{7}$,
∴$\frac {17}{5}≤n≤\frac {41}{7}$,
∵n为整数,
∴符合条件的n的整数值为4和5.
8.新课标模型观念「2023安徽芜湖二十九中一模」某景观公园的人工湖里有一组喷泉,水柱从垂直于湖面的水枪喷出,水柱在湖面上方的路径呈抛物线形.现测量出下表中的数据,在距水枪水平距离为d(米)的地点,水柱距离湖面的高度为h(米).
| d/米 | 0 | 0.7 | 2 | 3 | 4 | … |
| h/米 | 2.0 | 3.484 | 5.2 | 5.6 | 5.2 | … |
请解决以下问题:
(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线顺次连接.
(2)观察(1)中作出的曲线,其近似为抛物线.
①求抛物线的表达式.
②求喷泉的落水点距水枪的水平距离.
(3)已知喷泉喷出的水柱刚好没有落到人工湖岸上,如果改变喷泉的推力大小,使得喷出的水柱形成的抛物线为$h= -0.3(d-3.5)^{2}+5.7$,那么此时喷泉喷出的水柱是否会落到人工湖岸上?为什么?
(4)在(2)的条件下,公园增设了新的游玩项目,购置了宽度为4米,顶棚到湖面高度为4.2米的平顶游船,游船从喷泉最高处的正下方通过,别有一番趣味,请通过计算说明游船是否有被喷泉淋到的危险.

| d/米 | 0 | 0.7 | 2 | 3 | 4 | … |
| h/米 | 2.0 | 3.484 | 5.2 | 5.6 | 5.2 | … |
请解决以下问题:
(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线顺次连接.
(2)观察(1)中作出的曲线,其近似为抛物线.
①求抛物线的表达式.
②求喷泉的落水点距水枪的水平距离.
(3)已知喷泉喷出的水柱刚好没有落到人工湖岸上,如果改变喷泉的推力大小,使得喷出的水柱形成的抛物线为$h= -0.3(d-3.5)^{2}+5.7$,那么此时喷泉喷出的水柱是否会落到人工湖岸上?为什么?
(4)在(2)的条件下,公园增设了新的游玩项目,购置了宽度为4米,顶棚到湖面高度为4.2米的平顶游船,游船从喷泉最高处的正下方通过,别有一番趣味,请通过计算说明游船是否有被喷泉淋到的危险.

答案:
(1)如图.
(2)①由图象及表中数据可得,抛物线的顶点坐标为(3,5.6),
∴可设抛物线的表达式为$h=a(d-3)^{2}+5.6$,把(0,2.0)代入可得a=−0.4,
∴$h=-0.4(d-3)^{2}+5.6$.②当h=0时,$-0.4(d-3)^{2}+5.6=0$,解得$d=3+\sqrt{14}$或$d=3-\sqrt{14}$(舍去),
∴喷泉的落水点距水枪的水平距离为$(3+\sqrt{14})$米.
(3)会.理由:
∵−0.3>−0.4,|−0.3|<|−0.4|,
∴改变喷泉的推力后抛物线开口变大,再结合抛物线顶点坐标的变动,可知此时喷泉喷出的水柱会落到人工湖岸上.
(4)当$d=3+\frac{4}{2}=5$时,$h=-0.4×(5-3)^{2}+5.6=4<4.2$,
∴游船有被喷泉淋到的危险.
(1)如图.

(2)①由图象及表中数据可得,抛物线的顶点坐标为(3,5.6),
∴可设抛物线的表达式为$h=a(d-3)^{2}+5.6$,把(0,2.0)代入可得a=−0.4,
∴$h=-0.4(d-3)^{2}+5.6$.②当h=0时,$-0.4(d-3)^{2}+5.6=0$,解得$d=3+\sqrt{14}$或$d=3-\sqrt{14}$(舍去),
∴喷泉的落水点距水枪的水平距离为$(3+\sqrt{14})$米.
(3)会.理由:
∵−0.3>−0.4,|−0.3|<|−0.4|,
∴改变喷泉的推力后抛物线开口变大,再结合抛物线顶点坐标的变动,可知此时喷泉喷出的水柱会落到人工湖岸上.
(4)当$d=3+\frac{4}{2}=5$时,$h=-0.4×(5-3)^{2}+5.6=4<4.2$,
∴游船有被喷泉淋到的危险.
查看更多完整答案,请扫码查看


