《2025年5年中考3年模拟九年级数学上册沪科版》

10.「2023云南楚雄州二模」如图,在正方形网格中,每个小正方形的边长都是1,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正切值是( )

A.$\frac{\sqrt{5}}{5}$
B.$\frac{1}{5}$
C.$\frac{2\sqrt{5}}{5}$
D.$\frac{1}{2}$

答案： D　由题意得AB² = 3² + 4² = 25，BC² = 1² + 2² = 5，AC² = 2² + 4² = 20，
∴AC² + BC² = AB²，
∴△ABC是直角三角形，且∠ACB = 90°，
∴tan∠BAC = BC/AC = √5/√20 = √5/(2√5) = 1/2，故选D.

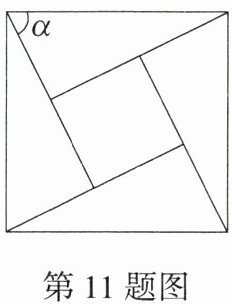
11.新数学文化「2022湖南湘潭中考」中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”。若“弦图”中小正方形的面积与每个直角三角形的面积均为1,α为直角三角形中的一个锐角,则tanα= ( )

A.2
B.$\frac{3}{2}$
C.$\frac{1}{2}$
D.$\frac{\sqrt{5}}{5}$

答案： A　由题意可得，大正方形的面积为1×4 + 1 = 5，设直角三角形中较长的直角边长为a，较短的直角边长为b，则a² + b² = 5，a - b = 1，解得a = 2，b = 1或a = -1，b = -2(不合题意，舍去)，
∴tanα = a/b = 2/1 = 2.

12.学科分类讨论思想「2025安徽合肥三十八中期中」定义：一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”,若等腰△ABC是“倍长三角形”,则底角的正切值为( )

A.$\frac{1}{4}$
B.$\frac{\sqrt{15}}{4}$
C.$\sqrt{15}$
D.$\frac{1}{2}$

答案：
C　在等腰△ABC中，设AB = AC.若等腰△ABC是“倍长三角形”，则存在以下两种情况:
①当BC = 2AB时，
∵AB + AC = BC，
∴线段AB，AC，BC不能组成三角形，与条件矛盾，此种情况不成立；
②当2BC = AB时，如图，过点A作AD⊥BC于点D，
∴BC = 2BD，
∴AB = 4BD.在Rt△ABD中，AD = √(AB² - BD²) = √15 BD，
∴tanB = AD/BD = √15 BD/BD = √15.
故选C.

13.「2024安徽亳州蒙城鲲鹏中学期末」在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,∠C= 90°,tanA= $\frac{1}{2}$,若c= 2,则a= ______。

答案： 答案 2√5/5
解析　在Rt△ABC中，∠C = 90°，tanA = 1/2，则a/b = 1/2，
∴b = 2a，
∵a² + b² = c²，c = 2，
∴a² + (2a)² = 2²，
∴a = 2√5/5.

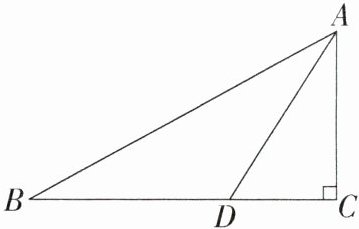
14.「2023安徽蚌埠五河期末」如图,在Rt△ABC中,∠C= 90°,BC= 8,tanB= $\frac{1}{2}$,点D在BC上,且BD= AD,求AC的长和tan∠ADC的值。

答案： 解析
∵在Rt△ABC中，∠C = 90°，BC = 8, tanB = 1/2，
∴AC/BC = 1/2，
∴AC = 4.设CD = x，则AD = BD = 8 - x，在Rt△ACD中，根据勾股定理得AD² = CD² + AC²，即(8 - x)² = x² + 16，解得x = 3，
∴CD = 3，
∴tan∠ADC = AC/CD = 4/3.

15.「」如图,某水库大坝的横截面是梯形,其迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝的高为20m,坝顶CD的宽为10m。求大坝横截面的周长。

答案：
解析　如图，作DE⊥AB于E，CF⊥AB于F，易知四边形CDEF是矩形，
∴EF = CD = 10m.由题意知DE = CF = 20m，DE∶AE = 4∶3，
∴AE = 15m，
∴AD = √(AE² + DE²) = 25(m)，
∵CF = 20m，CF∶BF = 1∶2，
∴BF = 40m，
∴BC = √(CF² + BF²) = 20√5(m).
∵AE = 15m，EF = 10m，BF = 40m，
∴AB = AE + EF + BF = 65m，
∴AD + DC + BC + AB = (100 + 20√5)m.
答：大坝横截面的周长为(100 + 20√5)m.

16.新几何直观新定义题如果三角形中一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”。若Rt△ABC是“好玩三角形”,且∠A= 90°,则tan∠ABC= ______。

答案：
答案 √3/2或2√3/3
解析　如图1，在Rt△ABC中，∠A = 90°，CE是△ABC的中线，设AB = EC = 2a，则AE = EB = a，AC = √3 a,
∴tan∠ABC = AC/AB = √3/2.如图2，在Rt△ABC中，∠A = 90°，BE是△ABC的中线，设EB = AC = 2a，则AE = EC = a，AB = √3 a，
∴tan∠ABC = AC/AB = 2√
(3)/3.综上，tan∠ABC = √3/2或2√3/3.