《2025年5年中考3年模拟九年级数学上册沪科版》

5.「2025安徽合肥四十五中期中」如图,E为□ABCD的边BA的延长线上一点,连接CE,交BD于点O,交AD于点F,求证：$\frac {OC}{OE}= \frac {OF}{OC}$.

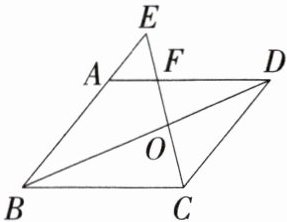
答案： 证明
∵四边形ABCD为平行四边形，
∴CD//BE，AD//BC，
∴△COD∽△EOB，△FOD∽△COB，
∴$\frac{CO}{EO}=\frac{DO}{BO}$，$\frac{OF}{OC}=\frac{DO}{BO}$，
∴$\frac{OC}{OE}=\frac{OF}{OC}$。

6.如图,CD是Rt△ABC斜边上的高,E为CB的中点,ED的延长线交CA的延长线于点F.求证：AC·CF= CB·DF.

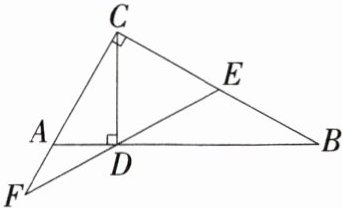
答案： 解析
∵CD⊥AB，
∴∠ADC=∠CDB=90°，
∵E为CB的中点，
∴$CE=EB=DE=\frac{1}{2}BC$，
∴∠B=∠BDE，
∵∠BDE=∠ADF，
∴∠B=∠ADF，
∵∠ACB=90°，
∴∠B+∠CAB=90°，
∵∠ACD+∠CAB=90°，
∴∠B=∠ACD，
∴∠ADF=∠ACD，
又
∵∠F=∠F，
∴△FDA∽△FCD，
∴$\frac{DF}{CF}=\frac{AD}{DC}$。
∵∠ADC=∠CDB=90°，∠ACD=∠B，
∴△ACD∽△CBD，
∴$\frac{AD}{DC}=\frac{AC}{CB}$，
∴$\frac{DF}{CF}=\frac{AC}{CB}$，即AC·CF=CB·DF。

7.如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F.求证：AE·AB= AF·AC.

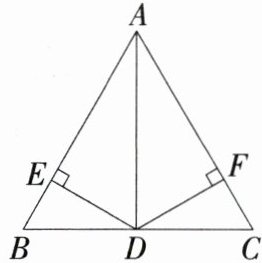
答案： 证明
∵AD⊥BC，
∴∠ADB=∠ADC=90°，
∵DE⊥AB，
∴∠AED=90°，
又
∵∠BAD=∠DAE，
∴△ABD∽△ADE，
∴$\frac{AD}{AE}=\frac{AB}{AD}$，
∴$AD^2=AE·AB$，
同理可得$AD^2=AF·AC$，
∴AE·AB=AF·AC。

8.如图,CE是Rt△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP于G,交CE于D.求证：$CE^2= PE·DE.$

答案： 证明　如图，
∵∠ACB=90°，CE⊥AB，
∴∠AEC=90°，∠ACE+∠BCE=90°，
∴∠ACE+∠CAE=90°，
∴∠CAE=∠BCE，
∴△ACE∽△CBE，
∴$\frac{CE}{BE}=\frac{AE}{CE}$，
∴$CE^2=AE·BE$。
∵BG⊥AP，CE⊥AB，
∴∠DEB=∠DGP=90°.
又
∵∠1=∠2，
∴∠P=∠3，
∴△AEP∽△DEB，
∴$\frac{PE}{BE}=\frac{AE}{DE}$，
∴PE·DE=AE·BE，
∴$CE^2=PE·DE$。