《2025年暑假作业知识出版社八年级数学人教版》

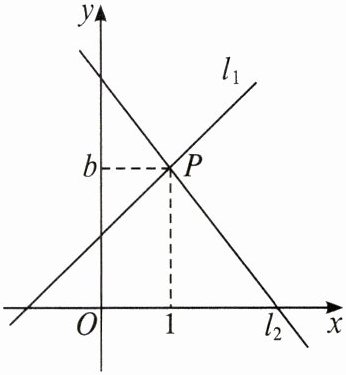
14. 如图，直线 $l_1:y = x + 1$ 与直线 $l_2:y = mx + n$ 相交于点 $P(1,b)$。
(1)求 $b$ 的值；2
(2)不解关于 $x$，$y$ 的方程组 $\begin{cases}y = x + 1,\\y = mx + n,\end{cases}$ 请你直接写出它的解；$\begin{cases} x=1 \\ y=2 \end{cases}$
(3)直线 $l_3:y = nx + m$ 是否也经过点 $P$？请说明理由。
直线 $y = nx + m$ 也经过点 $P$。理由如下：∵点 $P(1,2)$ 在直线 $y = mx + n$ 上，∴$m + n = 2$。对于直线 $l_3:y = nx + m$，将点 $(1,2)$ 代入，得 $m + n = 2$。故直线 $l_3:y = nx + m$ 也经过点 $P$。

答案： 解:
(1)由题知点 $ P ( 1, b ) $ 在直线 $ y = x + 1 $ 上,则 $ b = 1 + 1 = 2 $,故 $ b $ 的值为 2.
(2) $ \left\{ \begin{array} { l } { x = 1, } \\ { y = 2. } \end{array} \right. $
(3)直线 $ y = n x + m $ 也经过点 $ P $.
理由如下:
∵点 $ P ( 1, 2 ) $ 在直线 $ y = m x + n $ 上,
∴ $ m + n = 2 $.
对于直线 $ l _ { 3 } : y = n x + m $,将点 $ ( 1, 2 ) $ 代入,得 $ m + n = 2 $.故直线 $ l _ { 3 } : y = n x + m $ 也经过点 $ P $.

15. 已知一次函数 $y = kx + b$ 的图象经过点 $(2,3)$，与 $y$ 轴相交于 $B(0,4)$，与 $x$ 轴交于点 $A$。求该一次函数的解析式及 $\triangle AOB$ 的面积。($O$ 为坐标原点)

答案： 解:由一次函数的图象过点 $ ( 2, 3 ) $, $ ( 0, 4 ) $,得 $ \left\{ \begin{array} { l } { 3 = 2 k + b, } \\ { 4 = b. } \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k = - \frac { 1 } { 2 }, } \\ { b = 4. } \end{array} \right. $
故一次函数的解析式为 $ y = - \frac { 1 } { 2 } x + 4 $.
当 $ y = 0 $ 时,得 $ - \frac { 1 } { 2 } x + 4 = 0 $,即 $ x = 8 $.
故点 $ A $ 为 $ ( 8, 0 ) $.
故 $ S _ { \triangle A O B } = \frac { 1 } { 2 } × 4 × 8 = 16 $.