8. 如果代数式$\sqrt {-m}+\frac {1}{\sqrt {mn}}$有意义,那么在平面直角坐标系中,点$P(m,n)$的位置在(
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
C
)A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
答案:
C
9. 若数轴上表示a的点在原点左侧,则化简$|2a+\sqrt {a^{2}}|$的结果是(
A. $-a$
B. $-3a$
C. $a$
D. $3a$
A
)A. $-a$
B. $-3a$
C. $a$
D. $3a$
答案:
A
10. 使式子$\sqrt {m-2}$有意义的最小整数m是
2
.
答案:
2
11. 实数a,b在数轴上的位置如图所示,化简:$\sqrt {a^{2}}+\sqrt {b^{2}}+\sqrt {(a+1)^{2}}+\sqrt {(b-1)^{2}}$=
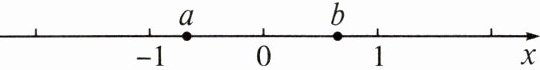
2
.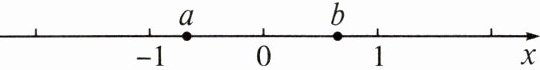
答案:
解: 由数轴可得 $-1 < a < 0, 0 < b < 1$, 故 $a + 1 > 0, b - 1 < 0$, 故原式 $= -a + b + a + 1 - (b - 1) = 2$.
12. 已知x,y为实数,且$y=\sqrt {x-4048}+\sqrt {4048-x}+1$,求$x+y$的值.
答案:
解: 由二次根式的定义, 知 $x - 4048 \geq 0$, 且 $4048 - x \geq 0$, 所以 $x = 4048$.
此时 $y = 1$, 所以 $x + y = 4049$.
此时 $y = 1$, 所以 $x + y = 4049$.
查看更多完整答案,请扫码查看


