《2025年暑假作业知识出版社八年级数学人教版》

1. 矩形具有而平行四边形不具有的性质是(B)
A. 对角相等
B. 对角线相等
C. 对角线互相平分
D. 对边平行且相等

答案： B

2. 下列图形既是轴对称图形,又是中心对称图形的是(C)
A. 平行四边形
B. 等边三角形
C. 矩形
D. 直角三角形

答案： C

3. 如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是(D)

A. $ AB = CD $
B. $ AD = BC $
C. $ AB = BC $
D. $ AC = BD $

答案： D

4. 下列说法正确的是(C)
A. 对角线互相垂直平分的四边形是矩形
B. 有两个角是直角的四边形是矩形
C. 对角线相等且互相平分的四边形是矩形
D. 矩形是对角线互相垂直且相等的四边形

答案： C

5. 若矩形的一条对角线与一边的夹角为$ 40^{\circ} $,则两条对角线相交所成的锐角是(D)
A. $ 20^{\circ} $
B. $ 40^{\circ} $
C. $ 60^{\circ} $
D. $ 80^{\circ} $

答案： D

6. 如图,矩形ABCD的对角线AC,BD相交于点O,过点O的直线分别交AD和BC于点E,F,$ AB = 2 $,$ BC = 3 $,求图中阴影部分的面积.

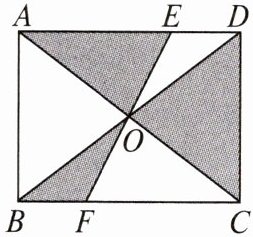
图中阴影部分的面积为3

答案： 1. 首先，证明$\triangle AOE\cong\triangle COF$：
因为四边形$ABCD$是矩形，所以$AD// BC$，$OA = OC$。
由$AD// BC$，可得$\angle OAE=\angle OCF$，$\angle OEA=\angle OFC$（两直线平行，内错角相等）。
在$\triangle AOE$和$\triangle COF$中，$\left\{\begin{array}{l}\angle OAE = \angle OCF\\\angle OEA=\angle OFC\\OA = OC\end{array}\right.$，根据$AAS$（角 - 角 - 边）定理，$\triangle AOE\cong\triangle COF$。
2. 然后，求阴影部分面积：
因为$\triangle AOE\cong\triangle COF$，所以$S_{\triangle AOE}=S_{\triangle COF}$。
那么阴影部分的面积$S_{阴影}=S_{\triangle AOE}+S_{\triangle BOF}+S_{\triangle COD}$，将$S_{\triangle AOE}=S_{\triangle COF}$代入可得$S_{阴影}=S_{\triangle BOC}+S_{\triangle COD}$。
又因为$S_{\triangle BOC}+S_{\triangle COD}=S_{\triangle BCD}$。
已知矩形$ABCD$中，$AB = 2$，$BC = 3$，根据矩形面积公式$S = AB× BC$，$S_{矩形ABCD}=AB× BC=2×3 = 6$。
而$S_{\triangle BCD}=\frac{1}{2}S_{矩形ABCD}$（矩形的对角线把矩形分成面积相等的两部分）。
所以$S_{阴影}=\frac{1}{2}×2×3 = 3$。
故图中阴影部分的面积为$3$。