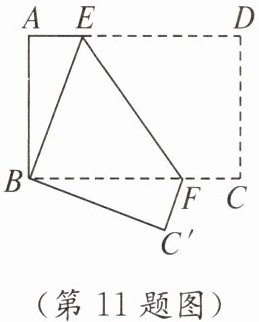
11. 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点$ C' $处,折痕为EF,若$ \angle ABE = 20^{\circ} $,则$ \angle EFC' $的度数为
125°
.
答案:
125°
12. 已知点M为矩形ABCD的边AD的中点,P为BC上的一点,且$ PE \perp MC $,$ PF \perp MB $,当AB,AD满足条件

AD=2AB
时,四边形PEMF是矩形.
答案:
AD=2AB
13. 如图,已知$ MN // PQ $,EF与MN,PQ分别交于A,C两点,过A,C两点作两组内错角的平分线,交于B,D两点,则四边形ABCD是
矩形
.
答案:
矩形
14. 如图,矩形ABCD的对角线相交于点O,E,F,G,H分别是AO,BO,CO,DO的中点,请问四边形EFGH是矩形吗? 请说明理由.
解:四边形EFGH是
∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO.
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EO=FO=GO=HO.
∴四边形EFGH是
∵EO+GO=FO+HO,∴EG=FH.
∴四边形EFGH是
解:四边形EFGH是
矩形
.理由如下:∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO.
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EO=FO=GO=HO.
∴四边形EFGH是
平行四边形
.∵EO+GO=FO+HO,∴EG=FH.
∴四边形EFGH是
矩形
.
答案:
解:四边形EFGH是矩形.理由如下:
∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO.
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EO=FO=GO=HO.
∴四边形EFGH是平行四边形.
∵EO+GO=FO+HO,
∴EG=FH.
∴四边形EFGH是矩形.
∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO.
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EO=FO=GO=HO.
∴四边形EFGH是平行四边形.
∵EO+GO=FO+HO,
∴EG=FH.
∴四边形EFGH是矩形.
15. 如图,$ DB // AC $,且$ DB = \frac{1}{2}AC $,E是AC的中点,
(1)求证:$ BC = DE $;
(2)连接AD,BE,若要使四边形DBEA是矩形,则需给$ \triangle ABC $添加什么条件? 为什么?

(1)求证:$ BC = DE $;
(2)连接AD,BE,若要使四边形DBEA是矩形,则需给$ \triangle ABC $添加什么条件? 为什么?

答案:
(1)证明:
∵E是AC的中点,
∴EC=$\frac{1}{2}$AC.
∵DB=$\frac{1}{2}$AC,
∴DB=EC.
∵DB//EC,
∴四边形DBCE是平行四边形.
∴BC=DE.
(2)解:添加AB=BC.
理由如下:如图所示.

∵DB$\equalparallel$AE,
∴四边形DBEA是平行四边形.
∵BC=DE,AB=BC,
∴AB=DE.
∴□ADBE是矩形.
(1)证明:
∵E是AC的中点,
∴EC=$\frac{1}{2}$AC.
∵DB=$\frac{1}{2}$AC,
∴DB=EC.
∵DB//EC,
∴四边形DBCE是平行四边形.
∴BC=DE.
(2)解:添加AB=BC.
理由如下:如图所示.

∵DB$\equalparallel$AE,
∴四边形DBEA是平行四边形.
∵BC=DE,AB=BC,
∴AB=DE.
∴□ADBE是矩形.
查看更多完整答案,请扫码查看


