1. 在平行四边形ABCD中,$∠B=60^{\circ }$,则下列各式中,不能成立的是(
A. $∠D=60^{\circ }$
B. $∠A=120^{\circ }$
C. $∠C+∠D=180^{\circ }$
D. $∠C+∠A=180^{\circ }$
D
)A. $∠D=60^{\circ }$
B. $∠A=120^{\circ }$
C. $∠C+∠D=180^{\circ }$
D. $∠C+∠A=180^{\circ }$
答案:
D
2. 用40cm长的绳子围成一个平行四边形,绳子无剩余,使其相邻两边的长度比为$3:2$,则较长边的长度为
12
cm.
答案:
12
3. 在$▱ABCD$中,$∠A+∠C=270^{\circ }$,则$∠B=$
$45^{\circ}$
,$∠C=$$135^{\circ}$
.
答案:
$45^{\circ}$ $135^{\circ}$
4. 如图,在$▱ABCD$中,$∠1=∠B=50^{\circ }$,则$∠2=$
$80^{\circ}$
.
答案:
$80^{\circ}$
5. 如图,在$▱ABCD$中,对角线AC,BD相交于点O,若$AC=14$,$BD=8$,$AB=10$,则$\triangle OAB$的周长为
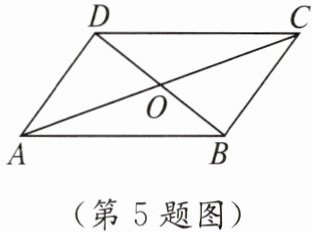
21
.
答案:
21
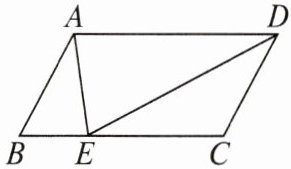
6. 如右图,已知平行四边形ABCD,DE是$∠ADC$的平分线,交BC于点E.
(1)求证:$CD=CE$;
(2)若$BE=CE$,$∠B=80^{\circ }$,求$∠DAE$的度数.
(1)求证:$CD=CE$;
(2)若$BE=CE$,$∠B=80^{\circ }$,求$∠DAE$的度数.

答案:
(1) 证明: 如图, 在$□ ABCD$中, $\because AD// BC$,
$\therefore \angle 1=\angle 3$.
又$\angle 1=\angle 2$,
$\therefore \angle 2=\angle 3$. $\therefore CD = CE$.

(2) 解: $\because$ 四边形 $ABCD$ 是平行四边形,
$\therefore AB = CD$. 又 $CD = CE$, $BE = CE$,
$\therefore AB = BE$. $\therefore \angle BAE=\angle BEA$.
$\because \angle B = 80^{\circ}$, $\therefore \angle BAE = 50^{\circ}$.
$\therefore \angle DAE = 180^{\circ}-80^{\circ}-50^{\circ}=50^{\circ}$.
(1) 证明: 如图, 在$□ ABCD$中, $\because AD// BC$,
$\therefore \angle 1=\angle 3$.
又$\angle 1=\angle 2$,
$\therefore \angle 2=\angle 3$. $\therefore CD = CE$.

(2) 解: $\because$ 四边形 $ABCD$ 是平行四边形,
$\therefore AB = CD$. 又 $CD = CE$, $BE = CE$,
$\therefore AB = BE$. $\therefore \angle BAE=\angle BEA$.
$\because \angle B = 80^{\circ}$, $\therefore \angle BAE = 50^{\circ}$.
$\therefore \angle DAE = 180^{\circ}-80^{\circ}-50^{\circ}=50^{\circ}$.
查看更多完整答案,请扫码查看


