《2025年暑假作业知识出版社八年级数学人教版》

8. 如图,学校在校园围墙边缘开垦一块四边形菜地ABCD,测得$AB=9m,BC=12m,CD=8m,AD=17m$,且$∠ABC=90^{\circ }$,则这块菜地的面积是(B)

A. $48m^{2}$
B. $114m^{2}$
C. $122m^{2}$
D. $158m^{2}$

答案： B

9. 已知a,b,c为$\triangle ABC$的三边,且满足$a^{2}c^{2}-b^{2}c^{2}=a^{4}-b^{4}$,试判断$\triangle ABC$的形状.
解:$\because a^{2}c^{2}-b^{2}c^{2}=a^{4}-b^{4},$ ①
$\therefore c^{2}(a^{2}-b^{2})=(a^{2}+b^{2})(a^{2}-b^{2}).$ ②
$\therefore c^{2}=a^{2}+b^{2}.$ ③
$\therefore \triangle ABC$是直角三角形.
问:
(1)上述解题过程是从哪一步开始出现错误的? 请写出该步的代号:③;
(2)错误原因是没有考虑$a^{2}-b^{2}=0$的情况;
(3)给出本题正确的结论.△ABC是直角三角形或等腰三角形。

答案：
(1)③;
(2)没有考虑$a^{2}-b^{2}=0$的情况;
(3)△ABC是直角三角形或等腰三角形。

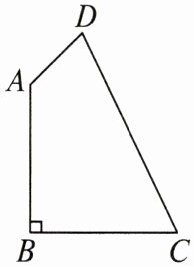
10. 如图,在四边形ABCD中,已知$AB:BC:CD:DA=2:2:3:1$,且$∠B=90^{\circ }$,求$∠DAB$的度数.

答案：
解:如图，连接AC.
设$AB = 2a$，则$BC = 2a$，$CD = 3a$，$DA = a$。

在Rt△ABC中,$AB = BC$，
所以$∠BAC = 45^{\circ}$。
$AC^{2}=AB^{2}+BC^{2}=(2a)^{2}+(2a)^{2}=8a^{2}$，
因为$AD^{2}+AC^{2}=a^{2}+8a^{2}=9a^{2}=(3a)^{2}=CD^{2}$，所以△ADC为直角三角形,$∠DAC = 90^{\circ}$。
所以$∠DAB = ∠DAC + ∠BAC = 90^{\circ}+45^{\circ}=135^{\circ}$。