《2025年暑假作业知识出版社八年级数学人教版》

16. 在数学活动课上,老师和同学们要判断一个四边形门框是不是矩形. 下面是某合作学习小组的四名同学拟定的方案,其中正确的是(D)
A. 测量对角线是否相互平分
B. 测量两组对边是否分别相等
C. 测量一组对角线是否垂直
D. 测量其中内角是否都为直角

答案： D

17. 工人师傅在做矩形零件时,常用测量平行四边形的两条对角线是否相等这一方法来检查直角的精度,这是根据对角线相等的平行四边形是矩形.

答案： 对角线相等的平行四边形是矩形

设计矩形时钟
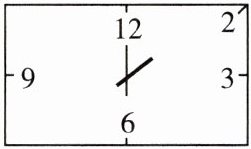
生活中常见的钟表是圆形的. 但在今天的课外活动课,富有创意的老师让同学们制作矩形表面. 要求矩形的宽为20cm,时钟的中心在矩形对角线的交点上,数字2在矩形的顶点上,数字3,6,9,12标在所在边的中点上,如图所示.
素有“小博士”之称的亮亮所在的小组最先有了制作思路. 他们发现需要先求出矩形的长,并且在矩形框上标出数字1的位置之后,利用对称性才可以在表框上标出其余的数字. 思路有了,他们就开始了计算.
同学们也试着动手计算一下吧!

答案：
$20\sqrt{3}cm$
分析：根据题意即可求得∠AOC = 2∠BOC，即可求得∠BOC = 30°，故OB = √3BC，即可求得矩形的长是宽的$\sqrt{3}$倍，即可解题。

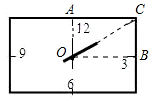
解答：解：由题意知∠AOC = 2∠BOC，
∵∠AOC + ∠BOC = 90°
∴∠BOC = 30°，∠AOC = 60°，
∴tanB = BC / OB = $\sqrt{3}$/ 3，
即OB = $\sqrt{3}$BC，
∴矩形ABCD长是宽的$\sqrt{3}$倍，
∵矩形的长是$20\sqrt{3}$厘米，
故答案为$20\sqrt{3}cm$。