《2025年暑假作业知识出版社八年级数学人教版》

1. 菱形具有而矩形不一定具有的性质是(B)
A. 两组对角分别相等
B. 对角线互相垂直
C. 对角线互相平分
D. 对角线相等

答案： B

2. 下列条件中,能判定四边形是菱形的是(C)
A. 两条对角线相等
B. 两条对角线互相垂直
C. 两条对角线互相垂直平分
D. 两条对角线相等且互相垂直

答案： C

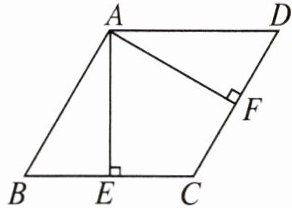
3. 在菱形 ABCD 中,$AE⊥BC$于点 E,$AF⊥CD$于点 F,且 E,F 分别为 BC,CD 的中点(如图),则$∠EAF$等于(B)

A. $75^{\circ }$
B. $60^{\circ }$
C. $45^{\circ }$
D. $30^{\circ }$

答案： B

4. 填空:
(1)对角线互相平分的四边形是平行四边形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线相等且互相平分的四边形是矩形;
(4)两组对边分别平行,且对角线互相垂直的四边形是菱形.

答案：
(1)平行四边形
(2)菱形
(3)矩形
(4)互相垂直

5. 在四边形 ABCD 中,已知$AB// CD,AD// BC$,请添加一个条件,使四边形 ABCD 是菱形,所添加的条件是$AB = AD$（答案不唯一）.

答案： $AB = AD$（答案不唯一）

6. 若菱形的一个内角是$120^{\circ }$,平分这个内角的一条对角线长为 13 cm,则菱形的周长是____52cm.

答案： $52\mathrm{cm}$

7. 如图,在菱形 ABCD 中,已知 E 是 BC 上一点,且$AE=AB,$$∠EAD=2∠BAE$,求证:$BF=AF.$
证明：$\because AE = AB$，$\therefore \angle ABE = \angle AEB$。
又 $AD // BC$，$\therefore \angle EAD = \angle AEB$。
$\because \angle EAD = 2 \angle BAE$，
$\therefore \angle AEB = 2 \angle BAE$。
$\therefore \angle ABE = 2 \angle BAE$。
$\because ABCD$ 是菱形，$\therefore BD$ 平分 $ \angle ABE$。
$\therefore \angle ABE = 2 \angle FBA$。
$\therefore \angle BAE = \angle FBA$，$\therefore BF = AF$。

答案： 证明：$\because AE = AB$，$\therefore \angle ABE = \angle AEB$。
又 $AD // BC$，$\therefore \angle EAD = \angle AEB$。
$\because \angle EAD = 2 \angle BAE$，
$\therefore \angle AEB = 2 \angle BAE$。
$\therefore \angle ABE = 2 \angle BAE$。
$\because ABCD$ 是菱形，$\therefore BD$ 平分 $ \angle ABE$。
$\therefore \angle ABE = 2 \angle FBA$。
$\therefore \angle BAE = \angle FBA$，$\therefore BF = AF$。