《2025年暑假作业知识出版社八年级数学人教版》

1. 下列函数中,是一次函数但不是正比例函数的为(C)
A. $ y = - \frac { x } { 2 } $
B. $ y = - \frac { 2 } { x } $
C. $ y = - \frac { x - 1 } { 2 } $
D. $ y = \frac { x ^ { 2 } - 1 } { x } $

答案： C

2. 一次函数 $ y = - 3 x - 2 $ 的图象不经过(A)
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： A

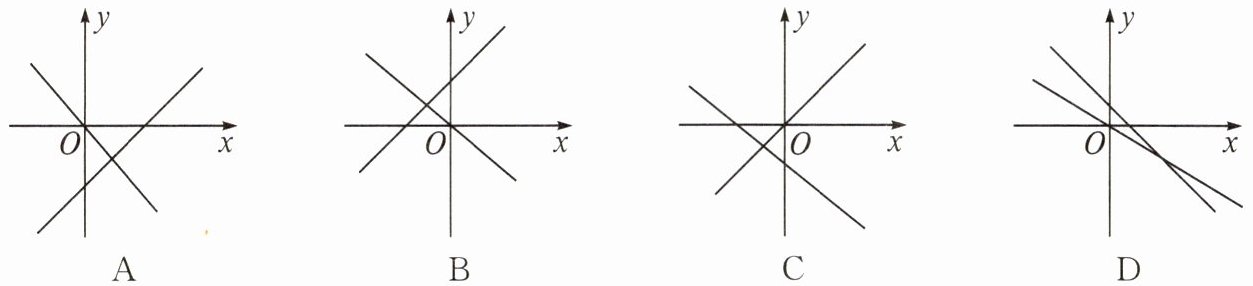
3. 下面表示一次函数 $ y = k x + b $ 与正比例函数 $ y = b x $ ( $ k , b $ 是常数,且 $ k \neq 0 $ )图象的是(A)

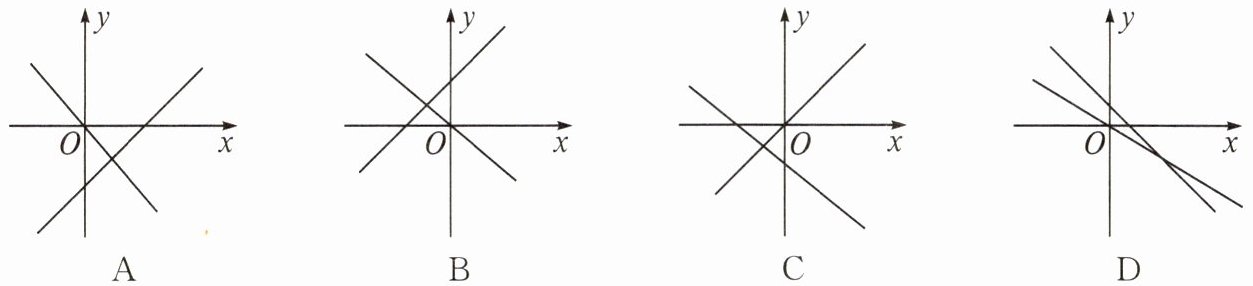
答案： A

4. 若点 $ P _ { 1 } ( x _ { 1 } , y _ { 1 } ) , P _ { 2 } ( x _ { 2 } , y _ { 2 } ) $ 是一次函数 $ y = - 4 x + 3 $ 图象上的两个点,且 $ x _ { 1 } ＜ x _ { 2 } $ ,则 $ y _ { 1 } $ 与 $ y _ { 2 } $ 的大小关系是(A)
A. $ y _ { 1 } ＞ y _ { 2 } $
B. $ y _ { 1 } ＞ y _ { 2 } ＞ 0 $
C. $ y _ { 1 } ＜ y _ { 2 } $
D. $ y _ { 1 } = y _ { 2 } $

答案： A

5. 已知地面气温是 $ 20 ^ { \circ } \mathrm { C } $ ,如果从地面开始,每升高 $ 1 \mathrm { km } $ ,气温下降 $ 6 ^ { \circ } \mathrm { C } $ ,那么气温 $ t $ (单位: $ ^ { \circ } \mathrm { C } $ )与海拔高度 $ h $ (单位: $ \mathrm { km } $ )的函数解析式是$ t = 20 - 6h $,它是一个一次函数.

答案： $ t = 20 - 6h $ 一次

6. 直线 $ y = \frac { 1 } { 3 } x + 5 $ 可以由直线 $ y = \frac { 1 } { 3 } x - 1 $ 向上平移6个单位得到.

答案： 上 6（答案不唯一）

7. 已知一次函数 $ y = ( 5 m - 3 ) x + ( 2 - n ) $ ,
(1)当 $ m $ 为何值时, $ y $ 随 $ x $ 的增大而减小?
(2)当 $ m , n $ 为何值时,一次函数的图象与 $ y $ 轴的交点在 $ x $ 轴的上方?
(3)当 $ m , n $ 为何值时,一次函数的图象经过第一、三、四象限?

答案： 解：
(1)由题意得 $ 5m - 3 ＜ 0 $，即 $ m ＜ \frac{3}{5} $，
于是当 $ m ＜ \frac{3}{5} $ 时，y 随 x 的增大而减小.
(2)由题意得 $ \begin{cases} 5m - 3 \neq 0, \\ 2 - n ＞ 0, \end{cases} $
故 $ m \neq \frac{3}{5} $，$ n ＜ 2 $，于是当 $ n ＜ 2 $，且 $ m \neq \frac{3}{5} $ 时，一次函数的图象与 y 轴的交点在 x 轴的上方.
(3)由题意得 $ \begin{cases} 5m - 3 ＞ 0, \\ 2 - n ＜ 0, \end{cases} $ 解得 $ m ＞ \frac{3}{5} $，且 $ n ＞ 2 $，于是当 $ m ＞ \frac{3}{5} $，且 $ n ＞ 2 $ 时，一次函数的图象经过第一、三、四象限.