《2025年暑假作业知识出版社八年级数学人教版》

8. 若函数 $ y = ( 2 m - 3 ) x + ( 3 n + 1 ) $ 的图象经过第一、二、三象限,则 $ m , n $ 的取值范围分别是(A)
A. $ m ＞ \frac { 3 } { 2 } , n ＞ - \frac { 1 } { 3 } $
B. $ m ＞ 3 , n ＞ - 3 $
C. $ m ＜ \frac { 3 } { 2 } , n ＜ - \frac { 1 } { 3 } $
D. $ m ＞ \frac { 3 } { 2 } , n ＜ \frac { 1 } { 3 } $

答案： A

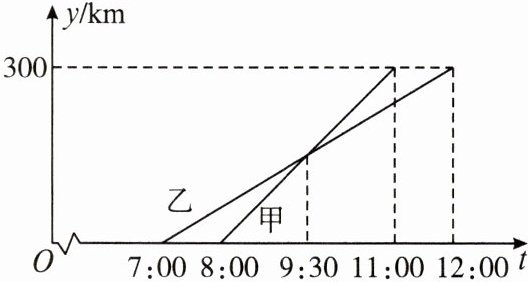
9. 甲、乙两车沿同一路线从 A 城出发前往 B 城,在整个行程中,汽车离开 A 城的路程 $ y $ 与时刻 $ t $ 的对应关系如图所示.关于下列结论:①A,B 两城相距 $ 300 \mathrm { km } $ ;②甲车的平均速度是 $ 60 \mathrm { km } / \mathrm { h } $ ,乙车的平均速度是 $ 100 \mathrm { km } / \mathrm { h } $ ;③乙车先出发,先到达 B 城;④甲车在 $ 9 : 30 $ 追上乙车.其中正确的有(①④)

A. ①②
B. ①③
C. ②④
D. ①④

答案： D 解析：由题中图象可知，A，B 两城相距 300 km，乙车先出发，甲车先到达 B 城，
故①符合题意，③不符合题意；
甲车的平均速度是 $ 300 ÷ 3 = 100(km/h) $，
乙车的平均速度是 $ 300 ÷ 5 = 60(km/h) $，
故②不符合题意；
设甲车出发后 x 小时，追上乙车，
$ 100x = 60(x + 1) $，
解得 $ x = 1.5 $.
∴甲车出发 1.5 小时后追上乙车.
∵甲车 $ 8:00 $ 出发，
∴甲车在 $ 9:30 $ 追上乙车.
故④符合题意.
综上所述，正确的有①④.

10. 如图,在平面直角坐标系中,直线 $ y = \frac { 3 } { 4 } x + 3 $ 交 $ x $ 轴于点 $ A $ 、交 $ y $ 轴于点 $ B $ ,动点 $ P $ 在 $ x $ 轴上,动点 $ Q $ 在线段 $ AB $ 上,满足 $ \angle B P Q = \angle B A O $ .当 $ \triangle P Q B $ 为等腰三角形时,点 $ P $ 的坐标是$ (4,0) $ 或 $ (1,0) $ 或 $ \left( -\frac{7}{8},0 \right) $.

答案： $ (4,0) $ 或 $ (1,0) $ 或 $ \left( -\frac{7}{8},0 \right) $

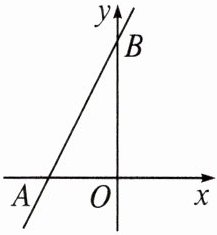
11. 如图,直线 $ y = 2 x + 3 $ 与 $ x $ 轴相交于点 $ A $ ,与 $ y $ 轴相交于点 $ B $ .
(1)求 $ A , B $ 两点的坐标;$ A $ 点坐标为$\left( -\frac{3}{2},0 \right)$，$ B $ 点坐标为$(0,3)$
(2)过 $ B $ 点作直线 $ B P $ 与 $ x $ 轴相交于点 $ P $ ,且使 $ O P = 2 O A $ ,求 $ \triangle A B P $ 的面积.$\frac{27}{4}$ 或 $\frac{9}{4}$

答案： 解：
(1)令 $ y = 0 $，得 $ x = -\frac{3}{2} $，
则 A 点坐标为 $ \left( -\frac{3}{2},0 \right) $.
令 $ x = 0 $，得 $ y = 3 $，则 B 点坐标为 $ (0,3) $.
(2)设 P 点坐标为 $ (x,0) $，依题意，得 $ x = \pm 3 $. 故 P 点坐标为 $ (3,0) $ 或 $ (-3,0) $，
那么 $ S_{\triangle ABP} = \frac{1}{2} × \left( \frac{3}{2} + 3 \right) × 3 = \frac{27}{4} $ 或 $ S_{\triangle ABP} = \frac{1}{2} × \left( 3 - \frac{3}{2} \right) × 3 = \frac{9}{4} $.
故 $ \triangle ABP $ 的面积为 $ \frac{27}{4} $ 或 $ \frac{9}{4} $.