11. 如图,钓鱼竿AB的长为5.4 m,露在水面上的鱼线BC长为1.8 m.当钓鱼者把钓鱼竿AB转到$AB'$的位置时,露在水面上的鱼线$B'C'$的长为4.2 m,求$CC'$的长.
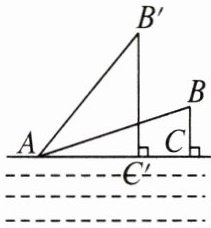
解:由题意可知,$AB' = AB = 5.4m$,$BC = 1.8m$,$B'C' = 4.2m$。
在Rt△ABC和Rt△AB'C'中,由勾股定理,得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{5.4^{2}-1.8^{2}}=$

解:由题意可知,$AB' = AB = 5.4m$,$BC = 1.8m$,$B'C' = 4.2m$。
在Rt△ABC和Rt△AB'C'中,由勾股定理,得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{5.4^{2}-1.8^{2}}=$
$\frac{18\sqrt{2}}{5}$
$(m)$,$AC'=\sqrt{AB'^{2}-B'C'^{2}}=\sqrt{5.4^{2}-4.2^{2}}=$$\frac{12\sqrt{2}}{5}$
$(m)$,$\therefore CC' = AC - AC'=$$\frac{18\sqrt{2}}{5}-\frac{12\sqrt{2}}{5}=\frac{6\sqrt{2}}{5}$
$(m)$。
答案:
解:由题意可知,$AB' = AB = 5.4m$,$BC = 1.8m$,$B'C' = 4.2m$。
在Rt△ABC和Rt△AB'C'中,由勾股定理,得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{5.4^{2}-1.8^{2}}=\frac{18\sqrt{2}}{5}(m)$,$AC'=\sqrt{AB'^{2}-B'C'^{2}}=\sqrt{5.4^{2}-4.2^{2}}=\frac{12\sqrt{2}}{5}(m)$,$\therefore CC' = AC - AC'=\frac{18\sqrt{2}}{5}-\frac{12\sqrt{2}}{5}=\frac{6\sqrt{2}}{5}(m)$。
在Rt△ABC和Rt△AB'C'中,由勾股定理,得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{5.4^{2}-1.8^{2}}=\frac{18\sqrt{2}}{5}(m)$,$AC'=\sqrt{AB'^{2}-B'C'^{2}}=\sqrt{5.4^{2}-4.2^{2}}=\frac{12\sqrt{2}}{5}(m)$,$\therefore CC' = AC - AC'=\frac{18\sqrt{2}}{5}-\frac{12\sqrt{2}}{5}=\frac{6\sqrt{2}}{5}(m)$。
查看更多完整答案,请扫码查看


