《2025年暑假作业知识出版社八年级数学人教版》

1. 正方形具有而矩形不一定具有的特征是(C)
A. 四个角都是直角
B. 对角线互相平分
C. 对角线互相垂直
D. 对角线相等

答案： C

2. 下列命题中,正确的是(D)
A. 四边相等的四边形是正方形
B. 四角相等的四边形是正方形
C. 对角线垂直的平行四边形是正方形
D. 对角线相等的菱形是正方形

答案： D

3. 如图,以A,B为顶点作位置不同的正方形,一共可以作(C)

A. 1个
B. 2个
C. 3个
D. 4个

答案： C

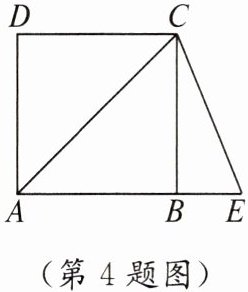
4. 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是22.5°.

答案： $22.5^{\circ}$

5. 在正方形ABCD中,AC为对角线,E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
证明: $ \because $ 四边形 $ ABCD $ 是正方形, $ \therefore BC = DC $. 又 $ AC $ 为对角线, $ E $ 为 $ AC $ 上一点, $ \therefore \angle BCE = \angle DCE = 45^{\circ} $. $ \because EC = EC $, $ \therefore \triangle BEC \cong \triangle DEC $ (SAS).
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
解: $ \because \triangle BEC \cong \triangle DEC $, $ \angle BED = 120^{\circ} $, $ \therefore \angle BEC = \angle DEC = 60^{\circ} $. $ \because \angle DAC = 45^{\circ} $, $ \therefore \angle ADE = 15^{\circ} $. $ \therefore \angle EFD = \angle BED - \angle ADE = 120^{\circ} - 15^{\circ} = $105°.

答案：
(1)证明: $ \because $ 四边形 $ ABCD $ 是正方形, $ \therefore BC = DC $. 又 $ AC $ 为对角线, $ E $ 为 $ AC $ 上一点, $ \therefore \angle BCE = \angle DCE = 45^{\circ} $. $ \because EC = EC $, $ \therefore \triangle BEC \cong \triangle DEC (SAS) $.
(2)解: $ \because \triangle BEC \cong \triangle DEC $, $ \angle BED = 120^{\circ} $, $ \therefore \angle BEC = \angle DEC = 60^{\circ} $. $ \because \angle DAC = 45^{\circ} $, $ \therefore \angle ADE = 15^{\circ} $. $ \therefore \angle EFD = \angle BED - \angle ADE = 120^{\circ} - 15^{\circ} = 105^{\circ} $.