《2025年假期园地暑假作业八年级数学人教版》

1. 已知菱形 $ABCD$ 中,对角线 $AC$ 与 $BD$ 相交于点 $O$,$\angle BAD = 120^{\circ}$,$AC = 4$,则该菱形的面积是(C)
A.$16\sqrt{3}$
B.$16$
C.$8\sqrt{3}$
D.$8$

答案： C

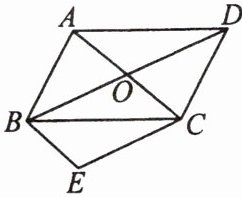
2. 如图所示,在平行四边形 $ABCD$ 中,对角线 $AC$,$BD$ 相交于点 $O$,将 $\triangle AOD$ 平移至 $\triangle BEC$ 的位置,则图中与 $OA$ 相等的线段有(B)

A.$1$ 条
B.$2$ 条
C.$3$ 条
D.$4$ 条

答案： B

3. 如图,将一个长为 $10cm$、宽为 $8cm$ 的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为(A)

A.$10cm^{2}$
B.$20cm^{2}$
C.$40cm^{2}$
D.$80cm^{2}$

答案： A

4. 在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$BC = 20cm$,$AC = 15cm$,则 $AB= $25cm。

答案： $25cm$

5. 当 $x$ 满足$x\geqslant-\frac{1}{2}$且$x\neq\frac{1}{5}$时,式子 $\frac{\sqrt{4x + 2}}{5x - 1}$ 有意义。

答案： $x\geqslant-\frac{1}{2}$且$x\neq\frac{1}{5}$

6. 若 $\sqrt{x - y - 2} + \sqrt{2x + y - 7} = 0$,则 $-\sqrt{x + y}= $$-2$。

答案： $-2$

7. 已知 $\sqrt[3a - 2b + 4]{5}$ 与 $\sqrt[2a - 3b + 10]{13}$ 都是最简二次根式,求 $a$,$b$ 的值。

答案： 【解析】：因为最简二次根式的根指数为$2$，所以对于$\sqrt[3a - 2b + 4]{5}$与$\sqrt[2a - 3b + 10]{13}$，可得到方程组$\begin{cases}3a - 2b + 4 = 2 \\2a - 3b + 10 = 2 \end{cases}$。
对第一个方程$3a - 2b + 4 = 2$进行化简可得$3a - 2b=-2$ ①；
对第二个方程$2a - 3b + 10 = 2$进行化简可得$2a - 3b=-8$ ②；
①$×3$得：$9a - 6b=-6$ ③；
②$×2$得：$4a - 6b=-16$ ④；
③$-$④得：$(9a - 6b)-(4a - 6b)=-6-(-16)$，即$9a - 6b - 4a + 6b=-6 + 16$，$5a = 10$，解得$a = 2$；
把$a = 2$代入①式得：$3×2 - 2b=-2$，$6 - 2b=-2$，$-2b=-2 - 6$，$-2b=-8$，解得$b = 4$。
【答案】：$a = 2$，$b = 4$