2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 已知$y与x - 3$成正比例,当$x = 4$,$y = 3$.
(1)写出$y与x$之间的函数关系式;
(2)求当$x = 2.5$时,$y$的值.
(1)写出$y与x$之间的函数关系式;
$y = 3x - 9$
(2)求当$x = 2.5$时,$y$的值.
$-1.5$
答案:
【解析】:
(1)因为$y$与$x - 3$成正比例,所以设$y=k(x - 3)$($k\neq0$)。
把$x = 4$,$y = 3$代入$y=k(x - 3)$中,可得$3=k×(4 - 3)$,即$3 = k×1$,解得$k = 3$。
把$k = 3$代入$y=k(x - 3)$,得到$y = 3(x - 3)=3x-9$,所以$y$与$x$之间的函数关系式是$y = 3x - 9$。
(2)当$x = 2.5$时,把$x = 2.5$代入$y = 3x - 9$中,$y=3×2.5-9=7.5 - 9=-1.5$。
【答案】:
(1)$y = 3x - 9$;
(2)$-1.5$
(1)因为$y$与$x - 3$成正比例,所以设$y=k(x - 3)$($k\neq0$)。
把$x = 4$,$y = 3$代入$y=k(x - 3)$中,可得$3=k×(4 - 3)$,即$3 = k×1$,解得$k = 3$。
把$k = 3$代入$y=k(x - 3)$,得到$y = 3(x - 3)=3x-9$,所以$y$与$x$之间的函数关系式是$y = 3x - 9$。
(2)当$x = 2.5$时,把$x = 2.5$代入$y = 3x - 9$中,$y=3×2.5-9=7.5 - 9=-1.5$。
【答案】:
(1)$y = 3x - 9$;
(2)$-1.5$
8. 如图,四边形$ABCD$中,$\angle A = \angle BCD = 90^{\circ}$,$BC = CD$,$CE \perp AD$,垂足为$E$.
求证:$AE = CE$.
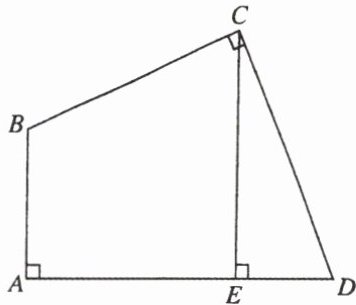
过点$B$作$BF\perp CE$于$F$。
$\because\angle BCD = 90^{\circ}$,$\therefore\angle BCF+\angle DCE = 90^{\circ}$。
$\because CE\perp AD$,$\therefore\angle D+\angle DCE = 90^{\circ}$,$\therefore\angle BCF=\angle D$。
$\because BF\perp CE$,$CE\perp AD$,$\angle A = 90^{\circ}$,$\therefore$四边形$AEFB$是矩形,$\angle BFC=\angle CED = 90^{\circ}$,$AE = BF$。
在$\triangle BCF$和$\triangle CDE$中,$\begin{cases}\angle BFC=\angle CED\\\angle BCF=\angle D\\BC = CD\end{cases}$,$\therefore\triangle BCF\cong\triangle CDE(AAS)$,$\therefore BF = CE$。
$\because AE = BF$,$\therefore AE = CE$。
求证:$AE = CE$.

过点$B$作$BF\perp CE$于$F$。
$\because\angle BCD = 90^{\circ}$,$\therefore\angle BCF+\angle DCE = 90^{\circ}$。
$\because CE\perp AD$,$\therefore\angle D+\angle DCE = 90^{\circ}$,$\therefore\angle BCF=\angle D$。
$\because BF\perp CE$,$CE\perp AD$,$\angle A = 90^{\circ}$,$\therefore$四边形$AEFB$是矩形,$\angle BFC=\angle CED = 90^{\circ}$,$AE = BF$。
在$\triangle BCF$和$\triangle CDE$中,$\begin{cases}\angle BFC=\angle CED\\\angle BCF=\angle D\\BC = CD\end{cases}$,$\therefore\triangle BCF\cong\triangle CDE(AAS)$,$\therefore BF = CE$。
$\because AE = BF$,$\therefore AE = CE$。
答案:
【解析】:
过点$B$作$BF\perp CE$于$F$。
因为$\angle BCD = 90^{\circ}$,所以$\angle BCF+\angle DCE = 90^{\circ}$。
又因为$CE\perp AD$,所以$\angle D+\angle DCE = 90^{\circ}$,则$\angle BCF=\angle D$。
因为$BF\perp CE$,$CE\perp AD$,$\angle A = 90^{\circ}$,所以四边形$AEFB$是矩形,$\angle BFC=\angle CED = 90^{\circ}$,$AE = BF$。
在$\triangle BCF$和$\triangle CDE$中,$\begin{cases}\angle BFC=\angle CED\\\angle BCF=\angle D\\BC = CD\end{cases}$,所以$\triangle BCF\cong\triangle CDE(AAS)$,则$BF = CE$。
因为$AE = BF$,所以$AE = CE$。
【答案】:
过点$B$作$BF\perp CE$于$F$。
$\because\angle BCD = 90^{\circ}$,$\therefore\angle BCF+\angle DCE = 90^{\circ}$。
$\because CE\perp AD$,$\therefore\angle D+\angle DCE = 90^{\circ}$,$\therefore\angle BCF=\angle D$。
$\because BF\perp CE$,$CE\perp AD$,$\angle A = 90^{\circ}$,$\therefore$四边形$AEFB$是矩形,$\angle BFC=\angle CED = 90^{\circ}$,$AE = BF$。
在$\triangle BCF$和$\triangle CDE$中,$\begin{cases}\angle BFC=\angle CED\\\angle BCF=\angle D\\BC = CD\end{cases}$,$\therefore\triangle BCF\cong\triangle CDE(AAS)$,$\therefore BF = CE$。
$\because AE = BF$,$\therefore AE = CE$。
过点$B$作$BF\perp CE$于$F$。
因为$\angle BCD = 90^{\circ}$,所以$\angle BCF+\angle DCE = 90^{\circ}$。
又因为$CE\perp AD$,所以$\angle D+\angle DCE = 90^{\circ}$,则$\angle BCF=\angle D$。
因为$BF\perp CE$,$CE\perp AD$,$\angle A = 90^{\circ}$,所以四边形$AEFB$是矩形,$\angle BFC=\angle CED = 90^{\circ}$,$AE = BF$。
在$\triangle BCF$和$\triangle CDE$中,$\begin{cases}\angle BFC=\angle CED\\\angle BCF=\angle D\\BC = CD\end{cases}$,所以$\triangle BCF\cong\triangle CDE(AAS)$,则$BF = CE$。
因为$AE = BF$,所以$AE = CE$。
【答案】:
过点$B$作$BF\perp CE$于$F$。
$\because\angle BCD = 90^{\circ}$,$\therefore\angle BCF+\angle DCE = 90^{\circ}$。
$\because CE\perp AD$,$\therefore\angle D+\angle DCE = 90^{\circ}$,$\therefore\angle BCF=\angle D$。
$\because BF\perp CE$,$CE\perp AD$,$\angle A = 90^{\circ}$,$\therefore$四边形$AEFB$是矩形,$\angle BFC=\angle CED = 90^{\circ}$,$AE = BF$。
在$\triangle BCF$和$\triangle CDE$中,$\begin{cases}\angle BFC=\angle CED\\\angle BCF=\angle D\\BC = CD\end{cases}$,$\therefore\triangle BCF\cong\triangle CDE(AAS)$,$\therefore BF = CE$。
$\because AE = BF$,$\therefore AE = CE$。
9. 某公司员工的月工资情况统计如下表:
|员工人数/人|2|4|8|20|8|4|
|月工资/元|5000|4000|2000|1500|1000|700|
(1)分别计算该公司月工资的平均数、中位数和众数.
(2)你认为用(1)中算出的哪个数据来表示该公司员工的月工资水平更为合适?
(3)请画出一种你认为合适的统计图来表示上面表格中的数据.
|员工人数/人|2|4|8|20|8|4|
|月工资/元|5000|4000|2000|1500|1000|700|
(1)分别计算该公司月工资的平均数、中位数和众数.
(2)你认为用(1)中算出的哪个数据来表示该公司员工的月工资水平更为合适?
(3)请画出一种你认为合适的统计图来表示上面表格中的数据.
答案:
【解析】:
1. 首先计算平均数:
平均数的计算公式为$\bar{x}=\frac{\sum_{i = 1}^{n}x_{i}f_{i}}{\sum_{i = 1}^{n}f_{i}}$,其中$x_{i}$是数据,$f_{i}$是对应数据的频数。
这里$\sum_{i = 1}^{n}f_{i}=2 + 4+8 + 20+8 + 4=46$(人)。
$\sum_{i = 1}^{n}x_{i}f_{i}=5000×2 + 4000×4+2000×8 + 1500×20+1000×8 + 700×4$
$=10000 + 16000+16000 + 30000+8000 + 2800$
$=82800$(元)。
则平均数$\bar{x}=\frac{82800}{46}=1800$(元)。
2. 然后求中位数:
一共有$46$个数据,将所有数据从小到大排列,中位数是第$23$个和第$24$个数据的平均数。
前$2 + 4+8 = 14$个数据是$5000$,$4000$,$2000$;从第$15$个到第$15 + 20=34$个数据是$1500$。
所以第$23$个和第$24$个数据都是$1500$,中位数为$\frac{1500 + 1500}{2}=1500$(元)。
3. 接着求众数:
众数是一组数据中出现次数最多的数据。
由表格可知$1500$元出现的次数最多,为$20$次,所以众数是$1500$元。
4. 对于用哪个数据表示该公司员工的月工资水平更为合适的问题:
平均数受极端值(如本题中的$5000$和$4000$)影响较大,该公司中大部分员工的工资都低于平均数,所以平均数不能很好地反映该公司员工的月工资水平。
中位数是按顺序排列的一组数据中居于中间位置的数,如果数据有奇数个,则正中间的数字为中位数;如果数据有偶数个,则中间两位数的平均数为中位数,它不受极端值的影响,能较好地反映中等水平。
众数是出现次数最多的数据,代表了数据的一般水平。在本题中,众数$1500$元是大多数员工的工资水平,所以用众数或中位数来表示该公司员工的月工资水平更为合适。
5. 关于统计图:
条形统计图的特点是能够清楚地表明各种数量的多少,所以用条形统计图来表示该公司员工的月工资情况比较合适。
【答案】:
(1)平均数是$1800$元,中位数是$1500$元,众数是$1500$元。
(2)用中位数或众数来表示该公司员工的月工资水平更为合适。
(3)用条形统计图来表示,横坐标表示月工资,纵坐标表示员工人数,根据表格数据画出对应的条形。
1. 首先计算平均数:
平均数的计算公式为$\bar{x}=\frac{\sum_{i = 1}^{n}x_{i}f_{i}}{\sum_{i = 1}^{n}f_{i}}$,其中$x_{i}$是数据,$f_{i}$是对应数据的频数。
这里$\sum_{i = 1}^{n}f_{i}=2 + 4+8 + 20+8 + 4=46$(人)。
$\sum_{i = 1}^{n}x_{i}f_{i}=5000×2 + 4000×4+2000×8 + 1500×20+1000×8 + 700×4$
$=10000 + 16000+16000 + 30000+8000 + 2800$
$=82800$(元)。
则平均数$\bar{x}=\frac{82800}{46}=1800$(元)。
2. 然后求中位数:
一共有$46$个数据,将所有数据从小到大排列,中位数是第$23$个和第$24$个数据的平均数。
前$2 + 4+8 = 14$个数据是$5000$,$4000$,$2000$;从第$15$个到第$15 + 20=34$个数据是$1500$。
所以第$23$个和第$24$个数据都是$1500$,中位数为$\frac{1500 + 1500}{2}=1500$(元)。
3. 接着求众数:
众数是一组数据中出现次数最多的数据。
由表格可知$1500$元出现的次数最多,为$20$次,所以众数是$1500$元。
4. 对于用哪个数据表示该公司员工的月工资水平更为合适的问题:
平均数受极端值(如本题中的$5000$和$4000$)影响较大,该公司中大部分员工的工资都低于平均数,所以平均数不能很好地反映该公司员工的月工资水平。
中位数是按顺序排列的一组数据中居于中间位置的数,如果数据有奇数个,则正中间的数字为中位数;如果数据有偶数个,则中间两位数的平均数为中位数,它不受极端值的影响,能较好地反映中等水平。
众数是出现次数最多的数据,代表了数据的一般水平。在本题中,众数$1500$元是大多数员工的工资水平,所以用众数或中位数来表示该公司员工的月工资水平更为合适。
5. 关于统计图:
条形统计图的特点是能够清楚地表明各种数量的多少,所以用条形统计图来表示该公司员工的月工资情况比较合适。
【答案】:
(1)平均数是$1800$元,中位数是$1500$元,众数是$1500$元。
(2)用中位数或众数来表示该公司员工的月工资水平更为合适。
(3)用条形统计图来表示,横坐标表示月工资,纵坐标表示员工人数,根据表格数据画出对应的条形。
查看更多完整答案,请扫码查看


