《2025年假期园地暑假作业八年级数学人教版》

8. 小明在微机课上设计了一幅长方形图片,已知长方形的长是$\sqrt{140\pi}cm$,宽是$\sqrt{35\pi}cm$,他又想设计一个面积与其相等的圆,请你帮助小明求出圆的半径。

答案： 【解析】：本题可先根据长方形的面积公式求出长方形图片的面积，再根据圆的面积公式列出关于圆半径的方程，最后求解方程得到圆的半径。
- **步骤一：计算长方形图片的面积**
根据长方形的面积公式$S = 长×宽$，已知长方形的长是$\sqrt{140\pi}cm$，宽是$\sqrt{35\pi}cm$，可得长方形图片的面积为：
$S_{长方形}=\sqrt{140\pi}×\sqrt{35\pi}$
根据二次根式乘法法则$\sqrt{a}\cdot\sqrt{b}=\sqrt{ab}$（$a\geq0,b\geq0$）对上式进行计算：
$S_{长方形}=\sqrt{140\pi×35\pi}=\sqrt{4900\pi^{2}} = 70\pi(cm^{2})$
- **步骤二：根据圆的面积公式列出关于半径的方程**
设圆的半径为$r cm$，根据圆的面积公式$S = \pi r^{2}$，已知圆的面积与长方形的面积相等，即$S_{圆}=S_{长方形}=70\pi cm^{2}$，可得方程：
$\pi r^{2}=70\pi$
- **步骤三：求解方程得到圆的半径**
方程两边同时除以$\pi$可得：$r^{2}=70$
因为半径$r\gt0$，所以对$r^{2}=70$两边同时开平方可得：$r = \sqrt{70}$
【答案】：$\sqrt{70}cm$

9. 如图所示,四边形$ABCD$中,$AB // CD$,$AC平分\angle BAD$,$CE // AD交AB于点E$。

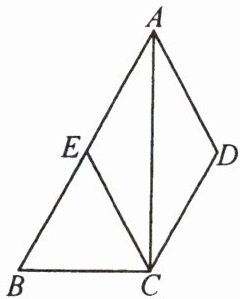
(1)求证：四边形$AECD$是菱形；
证明：因为$AB// CD$，$CE// AD$，所以四边形$AECD$是平行四边形。又因为$AC$平分$\angle BAD$，所以$\angle EAC = \angle DAC$。由于$AB// CD$，所以$\angle EAC = \angle ACD$，则$\angle DAC = \angle ACD$，所以$AD = CD$。一组邻边相等的平行四边形是菱形，所以四边形$AECD$是菱形。
(2)若点$E是AB$的中点,试判断$\triangle ABC$的形状。直角三角形

答案： 【解析】：
(1) 因为$AB// CD$，$CE// AD$，所以四边形$AECD$是平行四边形。
又因为$AC$平分$\angle BAD$，所以$\angle EAC = \angle DAC$。
由于$AB// CD$，所以$\angle EAC = \angle ACD$，则$\angle DAC = \angle ACD$，所以$AD = CD$。
一组邻边相等的平行四边形是菱形，所以四边形$AECD$是菱形。
(2) 因为点$E$是$AB$的中点，所以$AE = EB$。
又因为四边形$AECD$是菱形，所以$AE = EC$，则$EB = EC$，所以$\angle B = \angle ECB$。
因为$AE = EC$，所以$\angle EAC = \angle ECA$。
在$\triangle ABC$中，$\angle B+\angle ECB+\angle EAC+\angle ECA = 180^{\circ}$，即$2\angle ECB + 2\angle ECA = 180^{\circ}$，所以$\angle ECB+\angle ECA = 90^{\circ}$，即$\angle ACB = 90^{\circ}$，所以$\triangle ABC$是直角三角形。
【答案】：
(1) 证明见上述解析。
(2) $\triangle ABC$是直角三角形。