2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 如图所示,在$\triangle ABC$中,$AB= AC$,$AD$,$AE分别是∠BAC和∠BAC$外角的平分线,且$BE⊥AE$.
(1)求证:$DA⊥AE$;

(2)试判断$AB与DE$是否相等,并证明你的结论.
(1)求证:$DA⊥AE$;

因为$AD$平分$\angle BAC$,所以$\angle BAD=\frac{1}{2}\angle BAC$。又因为$AE$平分$\angle BAF$,所以$\angle BAE = \frac{1}{2}\angle BAF$。由于$\angle BAC+\angle BAF = 180^{\circ}$,那么$\angle BAD+\angle BAE=\frac{1}{2}(\angle BAC+\angle BAF)=\frac{1}{2}×180^{\circ}=90^{\circ}$,即$\angle DAE = 90^{\circ}$,所以$DA\perp AE$。
(2)试判断$AB与DE$是否相等,并证明你的结论.
$AB = DE$,证明:因为$AB = AC$,$AD$平分$\angle BAC$,根据等腰三角形三线合一,可得$AD\perp BC$,所以$\angle ADB = 90^{\circ}$。又因为$BE\perp AE$,$\angle DAE = 90^{\circ}$,所以四边形$ADBE$是矩形(有三个角是直角的四边形是矩形)。根据矩形的性质,矩形的对边相等,所以$AB = DE$。
答案:
【解析】:
(1) 因为$AD$平分$\angle BAC$,所以$\angle BAD=\frac{1}{2}\angle BAC$。
又因为$AE$平分$\angle BAF$,所以$\angle BAE = \frac{1}{2}\angle BAF$。
由于$\angle BAC+\angle BAF = 180^{\circ}$,那么$\angle BAD+\angle BAE=\frac{1}{2}(\angle BAC+\angle BAF)=\frac{1}{2}×180^{\circ}=90^{\circ}$,即$\angle DAE = 90^{\circ}$,所以$DA\perp AE$。
(2) 因为$AB = AC$,$AD$平分$\angle BAC$,根据等腰三角形三线合一,可得$AD\perp BC$,所以$\angle ADB = 90^{\circ}$。
又因为$BE\perp AE$,$\angle DAE = 90^{\circ}$,所以四边形$ADBE$是矩形(有三个角是直角的四边形是矩形)。
根据矩形的性质,矩形的对边相等,所以$AB = DE$。
【答案】:
(1) 证明见上述解析;
(2) $AB = DE$,证明见上述解析。
(1) 因为$AD$平分$\angle BAC$,所以$\angle BAD=\frac{1}{2}\angle BAC$。
又因为$AE$平分$\angle BAF$,所以$\angle BAE = \frac{1}{2}\angle BAF$。
由于$\angle BAC+\angle BAF = 180^{\circ}$,那么$\angle BAD+\angle BAE=\frac{1}{2}(\angle BAC+\angle BAF)=\frac{1}{2}×180^{\circ}=90^{\circ}$,即$\angle DAE = 90^{\circ}$,所以$DA\perp AE$。
(2) 因为$AB = AC$,$AD$平分$\angle BAC$,根据等腰三角形三线合一,可得$AD\perp BC$,所以$\angle ADB = 90^{\circ}$。
又因为$BE\perp AE$,$\angle DAE = 90^{\circ}$,所以四边形$ADBE$是矩形(有三个角是直角的四边形是矩形)。
根据矩形的性质,矩形的对边相等,所以$AB = DE$。
【答案】:
(1) 证明见上述解析;
(2) $AB = DE$,证明见上述解析。
9. 小亮和小莹自制了一个标靶进行投标比赛,两人各投了$10$次,如图是他们投标成绩的统计图.
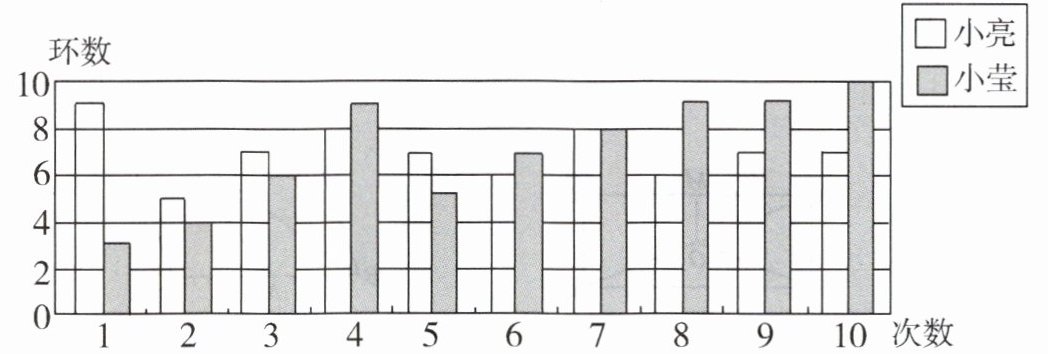
(1)根据图中信息填写下表:
| | 平均数 | 中位数 | 众数 |
| 小亮 |
| 小莹 | $7$ |
(2)分别用平均数和中位数解释谁的成绩比较好.
平均数:两人平均数相同,说明两人平均成绩一样;中位数:小莹中位数大于小亮中位数,说明小莹成绩较好。

(1)根据图中信息填写下表:
| | 平均数 | 中位数 | 众数 |
| 小亮 |
7
| $7$ | 7
|| 小莹 | $7$ |
7.5
| $9$ |(2)分别用平均数和中位数解释谁的成绩比较好.
平均数:两人平均数相同,说明两人平均成绩一样;中位数:小莹中位数大于小亮中位数,说明小莹成绩较好。
答案:
【解析】:
### (1)计算小亮的平均数、众数和小莹的中位数
**计算小亮的平均数**:
根据平均数公式$\bar{x}=\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}$(其中$n = 10$),小亮的成绩分别为$9$、$5$、$7$、$8$、$7$、$6$、$8$、$6$、$7$、$7$。
$\bar{x}_{小亮}=\frac{9 + 5+7+8+7+6+8+6+7+7}{10}=\frac{70}{10}=7$。
**计算小亮的众数**:
众数是一组数据中出现次数最多的数据。在小亮的成绩$9$、$5$、$7$、$8$、$7$、$6$、$8$、$6$、$7$、$7$中,$7$出现了$4$次,出现的次数最多,所以小亮成绩的众数是$7$。
**计算小莹的中位数**:
将小莹的成绩从小到大排列:$3$、$4$、$6$、$8$、$7$、$7$、$8$、$9$、$9$、$10$。
因为$n = 10$是偶数,根据中位数公式$M=\frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$($x_{\frac{n}{2}}$,$x_{\frac{n}{2}+1}$是按顺序排列后中间两个数),这里$x_{5}=7$,$x_{6}=8$,则中位数$M=\frac{7 + 8}{2}=7.5$。
### (2)用平均数和中位数解释成绩
**用平均数解释**:
小亮和小莹的平均数都是$7$,说明从平均水平看,两人成绩一样好。
**用中位数解释**:
小亮成绩的中位数是$7$,小莹成绩的中位数是$7.5$。中位数是将数据排序后位于中间位置的数,小莹成绩的中位数大于小亮成绩的中位数,说明小莹成绩中比中位数大的数更多,所以从中位数角度看,小莹的成绩比较好。
【答案】:
| | 平均数 | 中位数 | 众数 |
| 小亮 | $7$ | $7$ | $7$ |
| 小莹 | $7$ | $7.5$ | $9$ |
(2)平均数:两人平均数相同,说明两人平均成绩一样;中位数:小莹中位数大于小亮中位数,说明小莹成绩较好。
### (1)计算小亮的平均数、众数和小莹的中位数
**计算小亮的平均数**:
根据平均数公式$\bar{x}=\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}$(其中$n = 10$),小亮的成绩分别为$9$、$5$、$7$、$8$、$7$、$6$、$8$、$6$、$7$、$7$。
$\bar{x}_{小亮}=\frac{9 + 5+7+8+7+6+8+6+7+7}{10}=\frac{70}{10}=7$。
**计算小亮的众数**:
众数是一组数据中出现次数最多的数据。在小亮的成绩$9$、$5$、$7$、$8$、$7$、$6$、$8$、$6$、$7$、$7$中,$7$出现了$4$次,出现的次数最多,所以小亮成绩的众数是$7$。
**计算小莹的中位数**:
将小莹的成绩从小到大排列:$3$、$4$、$6$、$8$、$7$、$7$、$8$、$9$、$9$、$10$。
因为$n = 10$是偶数,根据中位数公式$M=\frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$($x_{\frac{n}{2}}$,$x_{\frac{n}{2}+1}$是按顺序排列后中间两个数),这里$x_{5}=7$,$x_{6}=8$,则中位数$M=\frac{7 + 8}{2}=7.5$。
### (2)用平均数和中位数解释成绩
**用平均数解释**:
小亮和小莹的平均数都是$7$,说明从平均水平看,两人成绩一样好。
**用中位数解释**:
小亮成绩的中位数是$7$,小莹成绩的中位数是$7.5$。中位数是将数据排序后位于中间位置的数,小莹成绩的中位数大于小亮成绩的中位数,说明小莹成绩中比中位数大的数更多,所以从中位数角度看,小莹的成绩比较好。
【答案】:
| | 平均数 | 中位数 | 众数 |
| 小亮 | $7$ | $7$ | $7$ |
| 小莹 | $7$ | $7.5$ | $9$ |
(2)平均数:两人平均数相同,说明两人平均成绩一样;中位数:小莹中位数大于小亮中位数,说明小莹成绩较好。
查看更多完整答案,请扫码查看


