《2025年假期园地暑假作业八年级数学人教版》

1. 化简$\sqrt {2}÷(\sqrt {2}-1)$的结果是 (D)
A.$2\sqrt {2}-1$
B.$2-\sqrt {2}$
C.$1-\sqrt {2}$
D.$2+\sqrt {2}$

答案： D

2. 若$(2+\sqrt {2})^{2}= a+b\sqrt {2}$($a$,$b$有理数),那么$a+b$等于 (D)
A.2
B.3
C.8
D.10

答案： D

3. 下列计算正确的是 (C)
A.$4\sqrt {3}-3\sqrt {3}= 1$
B.$\sqrt {2}+\sqrt {3}= \sqrt {5}$
C.$2\sqrt {\frac {1}{2}}= \sqrt {2}$
D.$3+2\sqrt {2}= 5\sqrt {2}$

答案： C

4. 一次函数的图象过点$(-1,0)$,且函数值随着自变量的增大而减小,写出一个符合以上条件的一次函数解析式$y=-x - 1$.

答案： $y=-x - 1$

5. 直线$y= kx+b经过A(2,1)$,$B(-1,-2)$两点时,则不等式$\frac {1}{2}＞kx+b＞-2$的解集为$-1\lt x\lt\frac{3}{2}$.

答案： $-1\lt x\lt\frac{3}{2}$

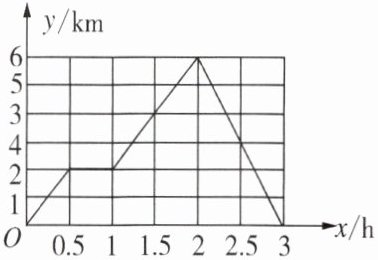
6. 如图所示的函数图象反映的过程：小明从家去书店,又去学校取信后马上回家,其中$x$表示时间(h),$y$表明小明离他家的距离(km),则小明往返的平均速度为4.8km/h.

答案： $4.8$

7. 有一块土地形状如图所示,$∠B= ∠D= 90^{\circ }$,$AB= 5\sqrt {3}m$,$BC= 3m$,$CD= 6\sqrt {2}m$,请计算这块地的面积.

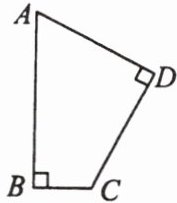
$\frac{15\sqrt{3}+12\sqrt{6}}{2}m^{2}$

答案： 【解析】：连接$AC$。
在$Rt\triangle ABC$中，$\angle B = 90^{\circ}$，$AB = 5\sqrt{3}m$，$BC = 3m$，根据勾股定理$AC^{2}=AB^{2}+BC^{2}$，则$AC=\sqrt{(5\sqrt{3})^{2}+3^{2}}=\sqrt{75 + 9}=\sqrt{84}=2\sqrt{21}m$。
$S_{\triangle ABC}=\frac{1}{2}× AB× BC=\frac{1}{2}×5\sqrt{3}×3=\frac{15\sqrt{3}}{2}m^{2}$。
在$Rt\triangle ADC$中，$\angle D = 90^{\circ}$，$CD = 6\sqrt{2}m$，$AC = 2\sqrt{21}m$，根据勾股定理$AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{(2\sqrt{21})^{2}-(6\sqrt{2})^{2}}=\sqrt{84 - 72}=\sqrt{12}=2\sqrt{3}m$。
$S_{\triangle ADC}=\frac{1}{2}× AD× CD=\frac{1}{2}×2\sqrt{3}×6\sqrt{2}=6\sqrt{6}m^{2}$。
这块地的面积$S = S_{\triangle ABC}+S_{\triangle ADC}=\frac{15\sqrt{3}}{2}+6\sqrt{6}=\frac{15\sqrt{3}+12\sqrt{6}}{2}m^{2}$。
【答案】：$\frac{15\sqrt{3}+12\sqrt{6}}{2}m^{2}$