2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 在$□ ABCD$中,$\angle BAD的平分线AE交BC于点E$,且$AE = BE$,则$\angle BCD$的度数是(
A.$30^{\circ}$
B.$60^{\circ}或120^{\circ}$
C.$60^{\circ}$
D.$120^{\circ}$
D
)A.$30^{\circ}$
B.$60^{\circ}或120^{\circ}$
C.$60^{\circ}$
D.$120^{\circ}$
答案:
D
2. 四边形的两条对角线分别长$12cm和10cm$,顺次连接各边中点,所得四边形的周长是(
A.$10cm$
B.$18cm$
C.$22cm$
D.$12cm$
C
)A.$10cm$
B.$18cm$
C.$22cm$
D.$12cm$
答案:
C
3. 如图,已知四边形$ABCD$为平行四边形,下列结论不一定正确的是(
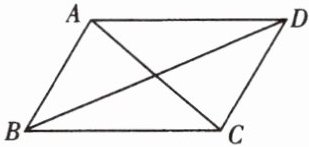
A.AB=CD
B.AC=BD
C.当$AC\perp BD$时,它是菱形
D.当$\angle AB$
B
)
A.AB=CD
B.AC=BD
C.当$AC\perp BD$时,它是菱形
D.当$\angle AB$
答案:
B
4. 某校八年级(2)班第一小组女生的体重(单位:$kg$)为:$38$,$40$,$35$,$36$,$65$,$42$,$42$,则这组数据的中位数是
40
。
答案:
$40$
5. 某校$5$个小组参加植树活动,平均每组植树$10$株,已知第一、二、三、四组分别植树$9$株、$12$株、$9$株、$8$株,那么第五小组植树
12
株。
答案:
$12$
6. 一组同学中,身高的极差为$22cm$,个子最高的同学身高为$175cm$,则个子最矮的同学身高为______
153cm
。
答案:
$153cm$
7. 先化简,再求值:$\frac{x - 3}{x - 2}÷(x + 2-\frac{5}{x - 2})$,其中$x = \sqrt{5}-3$。
答案:
【解析】:
本题可先化简原式,再将$x = \sqrt{5}-3$代入化简后的式子求值。
- **步骤一:化简原式**
先对括号内的式子进行通分计算:
$x + 2 - \frac{5}{x - 2}=\frac{(x + 2)(x - 2)}{x - 2}-\frac{5}{x - 2}$
根据平方差公式$(a+b)(a-b)=a^2-b^2$对上式分子进行化简:
$\frac{(x + 2)(x - 2)}{x - 2}-\frac{5}{x - 2}=\frac{x^2 - 4 - 5}{x - 2}=\frac{x^2 - 9}{x - 2}$
再根据平方差公式$a^2-b^2=(a+b)(a-b)$进一步化简分子:
$\frac{x^2 - 9}{x - 2}=\frac{(x + 3)(x - 3)}{x - 2}$
此时原式变为$\frac{x - 3}{x - 2} ÷ \frac{(x + 3)(x - 3)}{x - 2}$,根据除法运算法则,除以一个数等于乘以它的倒数,则有:
$\frac{x - 3}{x - 2} ÷ \frac{(x + 3)(x - 3)}{x - 2}=\frac{x - 3}{x - 2} × \frac{x - 2}{(x + 3)(x - 3)}$
约分可得:$\frac{1}{x + 3}$
- **步骤二:代入求值**
将$x = \sqrt{5}-3$代入$\frac{1}{x + 3}$可得:
$\frac{1}{\sqrt{5}-3 + 3}=\frac{1}{\sqrt{5}}$
分母有理化,给分子分母同时乘以$\sqrt{5}$:
$\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$
【答案】:化简结果为$\frac{1}{x + 3}$,值为$\frac{\sqrt{5}}{5}$
本题可先化简原式,再将$x = \sqrt{5}-3$代入化简后的式子求值。
- **步骤一:化简原式**
先对括号内的式子进行通分计算:
$x + 2 - \frac{5}{x - 2}=\frac{(x + 2)(x - 2)}{x - 2}-\frac{5}{x - 2}$
根据平方差公式$(a+b)(a-b)=a^2-b^2$对上式分子进行化简:
$\frac{(x + 2)(x - 2)}{x - 2}-\frac{5}{x - 2}=\frac{x^2 - 4 - 5}{x - 2}=\frac{x^2 - 9}{x - 2}$
再根据平方差公式$a^2-b^2=(a+b)(a-b)$进一步化简分子:
$\frac{x^2 - 9}{x - 2}=\frac{(x + 3)(x - 3)}{x - 2}$
此时原式变为$\frac{x - 3}{x - 2} ÷ \frac{(x + 3)(x - 3)}{x - 2}$,根据除法运算法则,除以一个数等于乘以它的倒数,则有:
$\frac{x - 3}{x - 2} ÷ \frac{(x + 3)(x - 3)}{x - 2}=\frac{x - 3}{x - 2} × \frac{x - 2}{(x + 3)(x - 3)}$
约分可得:$\frac{1}{x + 3}$
- **步骤二:代入求值**
将$x = \sqrt{5}-3$代入$\frac{1}{x + 3}$可得:
$\frac{1}{\sqrt{5}-3 + 3}=\frac{1}{\sqrt{5}}$
分母有理化,给分子分母同时乘以$\sqrt{5}$:
$\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$
【答案】:化简结果为$\frac{1}{x + 3}$,值为$\frac{\sqrt{5}}{5}$
查看更多完整答案,请扫码查看


