2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 计算 $ 4 \sqrt { \frac { 1 } { 2 } } + 3 \sqrt { \frac { 1 } { 3 } } - \sqrt { 8 } $ 的结果是 (
A.$ \sqrt { 3 } + \sqrt { 2 } $
B.$ \sqrt { 3 } $
C.$ \frac { \sqrt { 3 } } { 8 } $
D.$ \sqrt { 3 } - \sqrt { 2 } $
B
)A.$ \sqrt { 3 } + \sqrt { 2 } $
B.$ \sqrt { 3 } $
C.$ \frac { \sqrt { 3 } } { 8 } $
D.$ \sqrt { 3 } - \sqrt { 2 } $
答案:
B
2. 设实数 $ a, b $ 在数轴上对应的位置如图所示,化简 $ \sqrt { a ^ { 2 } } + | a + b | $ 的结果是 (
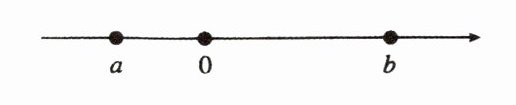
A.$ - 2 a + b $
B.$ 2 a + b $
C.$ - b $
D.$ b $
D
)
A.$ - 2 a + b $
B.$ 2 a + b $
C.$ - b $
D.$ b $
答案:
D
3. 在平行四边形 $ A B C D $ 中,两条邻边的差为 $ 4 \mathrm { cm } $,周长为 $ 32 \mathrm { cm } $,则两条邻边长分别为
10cm和6cm
.
答案:
$10cm$和$6cm$
4. 在 $ □ A B C D $ 中,$ \angle A - \angle B = 40 ^ { \circ } $,则 $ \angle A = $______
$110^{\circ}$
,$ \angle C = $______$110^{\circ}$
.
答案:
$110^{\circ}$,$110^{\circ}$
5. $ □ A B C D $ 的对角线 $ A C, B D $ 相交于点 $ O $,如果 $ □ A B C D $ 的面积为 $ 12 \mathrm { cm } ^ { 2 } $,则 $ \triangle B C D $ 的面积是______
6cm²
.
答案:
$6cm^2$
6. $ □ A B C D $ 中,$ E F $ 交 $ A B, C D $ 于点 $ E, F $;$ G H $ 交 $ A D, B C $ 于点 $ G, H $. 如果 $ E F // A D $,$ G H // C D $,$ E F $ 与 $ G H $ 相交于点 $ O $. 那么图中的平行四边形一共有
9
个.
答案:
$9$
7. 先化简,再求值:$ ( \frac { x + 2 } { x ^ { 2 } - 2 x } - \frac { x - 1 } { x ^ { 2 } - 4 x + 4 } ) ÷ \frac { x ^ { 2 } - 16 } { x ^ { 2 } + 4 x } $,其中 $ x = 2 + \sqrt { 2 } $.
答案:
【解析】:
本题可先对原式中括号内的式子进行通分,再将除法运算转化为乘法运算,然后进行化简,最后将$x = 2 + \sqrt { 2 }$代入化简后的式子求值。
- **步骤一:对原式中括号内的式子进行通分**
对$\frac{x + 2}{x^2 - 2x}$和$\frac{x - 1}{x^2 - 4x + 4}$分别化简:
对$\frac{x + 2}{x^2 - 2x}$,提取公因式$x$可得$\frac{x + 2}{x(x - 2)}$。
对$\frac{x - 1}{x^2 - 4x + 4}$,根据完全平方公式$(a-b)^2=a^2-2ab+b^2$可得$\frac{x - 1}{(x - 2)^2}$。
则$(\frac{x + 2}{x^2 - 2x} - \frac{x - 1}{x^2 - 4x + 4})$通分可得:
$\left[\frac{(x + 2)(x - 2)}{x(x - 2)^2} - \frac{x(x - 1)}{x(x - 2)^2}\right]=\frac{(x + 2)(x - 2)-x(x - 1)}{x(x - 2)^2}$
根据平方差公式$(a+b)(a-b)=a^2-b^2$对上式分子展开可得:
$\frac{x^2 - 4 - (x^2 - x)}{x(x - 2)^2}=\frac{x^2 - 4 - x^2 + x}{x(x - 2)^2}=\frac{x - 4}{x(x - 2)^2}$
- **步骤二:将除法运算转化为乘法运算并化简**
将原式中的除法运算$÷\frac{x^2 - 16}{x^2 + 4x}$转化为乘法运算,即乘以除数的倒数:
$\frac{x - 4}{x(x - 2)^2}×\frac{x^2 + 4x}{x^2 - 16}$
对$x^2 + 4x$提取公因式$x$可得$x(x + 4)$,对$x^2 - 16$根据平方差公式可得$(x + 4)(x - 4)$,则上式可化为:
$\frac{x - 4}{x(x - 2)^2}×\frac{x(x + 4)}{(x + 4)(x - 4)}=\frac{1}{(x - 2)^2}$
- **步骤三:代入$x$的值求值**
将$x = 2 + \sqrt { 2 }$代入$\frac{1}{(x - 2)^2}$可得:
$\frac{1}{(2 + \sqrt { 2 } - 2)^2}=\frac{1}{(\sqrt { 2 })^2}=\frac{1}{2}$
【答案】:$\frac{1}{2}$
本题可先对原式中括号内的式子进行通分,再将除法运算转化为乘法运算,然后进行化简,最后将$x = 2 + \sqrt { 2 }$代入化简后的式子求值。
- **步骤一:对原式中括号内的式子进行通分**
对$\frac{x + 2}{x^2 - 2x}$和$\frac{x - 1}{x^2 - 4x + 4}$分别化简:
对$\frac{x + 2}{x^2 - 2x}$,提取公因式$x$可得$\frac{x + 2}{x(x - 2)}$。
对$\frac{x - 1}{x^2 - 4x + 4}$,根据完全平方公式$(a-b)^2=a^2-2ab+b^2$可得$\frac{x - 1}{(x - 2)^2}$。
则$(\frac{x + 2}{x^2 - 2x} - \frac{x - 1}{x^2 - 4x + 4})$通分可得:
$\left[\frac{(x + 2)(x - 2)}{x(x - 2)^2} - \frac{x(x - 1)}{x(x - 2)^2}\right]=\frac{(x + 2)(x - 2)-x(x - 1)}{x(x - 2)^2}$
根据平方差公式$(a+b)(a-b)=a^2-b^2$对上式分子展开可得:
$\frac{x^2 - 4 - (x^2 - x)}{x(x - 2)^2}=\frac{x^2 - 4 - x^2 + x}{x(x - 2)^2}=\frac{x - 4}{x(x - 2)^2}$
- **步骤二:将除法运算转化为乘法运算并化简**
将原式中的除法运算$÷\frac{x^2 - 16}{x^2 + 4x}$转化为乘法运算,即乘以除数的倒数:
$\frac{x - 4}{x(x - 2)^2}×\frac{x^2 + 4x}{x^2 - 16}$
对$x^2 + 4x$提取公因式$x$可得$x(x + 4)$,对$x^2 - 16$根据平方差公式可得$(x + 4)(x - 4)$,则上式可化为:
$\frac{x - 4}{x(x - 2)^2}×\frac{x(x + 4)}{(x + 4)(x - 4)}=\frac{1}{(x - 2)^2}$
- **步骤三:代入$x$的值求值**
将$x = 2 + \sqrt { 2 }$代入$\frac{1}{(x - 2)^2}$可得:
$\frac{1}{(2 + \sqrt { 2 } - 2)^2}=\frac{1}{(\sqrt { 2 })^2}=\frac{1}{2}$
【答案】:$\frac{1}{2}$
查看更多完整答案,请扫码查看


