《2025年假期园地暑假作业八年级数学人教版》

8. 已知一次函数 $y = kx + b$ 的图象经过 $(0,2)$,$(1,3)$ 两点。
(1) 求 $k$,$b$ 的值；$k=$1，$b=$2
(2) 若一次函数 $y = kx + b$ 的图象与 $x$ 轴的交点为 $A(a,0)$,求 $a$ 的值。$a=$-2

答案： 【解析】：
(1) 已知一次函数$y = kx + b$的图象经过$(0,2)$，$(1,3)$两点。
把$(0,2)$代入$y = kx + b$中，可得：
当$x = 0$，$y = 2$时，$2=k×0 + b$，解得$b = 2$。
把$(1,3)$和$b = 2$代入$y = kx + b$中，可得：
当$x = 1$，$y = 3$，$b = 2$时，$3=k×1 + 2$，即$k+2 = 3$，移项可得$k=3 - 2=1$。
(2) 由
(1)可知一次函数的解析式为$y=x + 2$。
因为一次函数$y = kx + b$的图象与$x$轴的交点为$A(a,0)$，即当$y = 0$时，$x=a$。
把$y = 0$代入$y=x + 2$中，可得$0=a + 2$，移项解得$a=-2$。
【答案】：
(1)$k = 1$，$b = 2$；
(2)$a=-2$

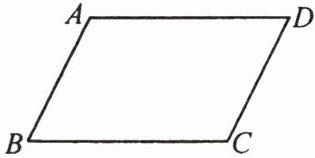
9. 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形 $ABCD$ 是平行四边形,并予以证明。(写出一种即可)
关系：① $AD// BC$,② $AB = CD$,③ $\angle A = \angle C$,④ $\angle B + \angle C = 180^{\circ}$。
已知：在四边形 $ABCD$ 中,①,③。
求证：四边形 $ABCD$ 是平行四边形。

答案： 【解析】：
若选条件①$AD// BC$和③$\angle A=\angle C$。
因为$AD// BC$，所以$\angle A+\angle B = 180^{\circ}$（两直线平行，同旁内角互补）。
又因为$\angle A=\angle C$，所以$\angle C+\angle B = 180^{\circ}$，则$AB// CD$（同旁内角互补，两直线平行）。
因为$AD// BC$且$AB// CD$，所以四边形$ABCD$是平行四边形（两组对边分别平行的四边形是平行四边形）。
若选条件①$AD// BC$和④$\angle B+\angle C = 180^{\circ}$。
因为$\angle B+\angle C = 180^{\circ}$，所以$AB// CD$（同旁内角互补，两直线平行）。
又因为$AD// BC$，所以四边形$ABCD$是平行四边形（两组对边分别平行的四边形是平行四边形）。
若选条件②$AB = CD$和④$\angle B+\angle C = 180^{\circ}$。
因为$\angle B+\angle C = 180^{\circ}$，所以$AB// CD$（同旁内角互补，两直线平行）。
又因为$AB = CD$，所以四边形$ABCD$是平行四边形（一组对边平行且相等的四边形是平行四边形）。
若选条件③$\angle A=\angle C$和④$\angle B+\angle C = 180^{\circ}$。
因为$\angle B+\angle C = 180^{\circ}$，所以$AB// CD$（同旁内角互补，两直线平行），则$\angle A+\angle D=180^{\circ}$（两直线平行，同旁内角互补）。
又因为$\angle A=\angle C$，所以$\angle C+\angle D = 180^{\circ}$，则$AD// BC$（同旁内角互补，两直线平行）。
因为$AB// CD$且$AD// BC$，所以四边形$ABCD$是平行四边形（两组对边分别平行的四边形是平行四边形）。
【答案】：
①，③（或①，④或②，④或③，④）。