2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 在平行四边形ABCD中,$AB = AC = AD$,$BC = CD$,$\angle BAC$的平分线AE交BC于点E,AF是CD边上的中线,$PC\perp CD$交AE于点P,$QC\perp BC$交AF于点Q,求证:四边形APCQ是菱形.
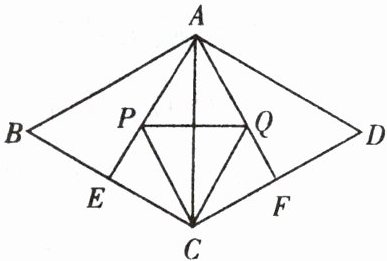
证明:
- 因为$AB = AC$,$AE$平分$\angle BAC$,根据等腰三角形三线合一,可得
- 又因为$AC = AD$,$AF$是$CD$边上的中线,同理可得
- 已知$BC = CD$,所以
- 因为$PC\perp CD$,$QC\perp BC$,$\angle BCD=\angle BCD$,所以
- 在$\triangle PCE$和$\triangle QCF$中,$\left\{\begin{array}{l}\angle PEC=\angle QFC = 90^{\circ}\\EC = FC\\\angle PCE=\angle QCF\end{array}\right.$,根据
- 因为$AE\perp BC$,$QC\perp BC$,所以
- 又因为

证明:
- 因为$AB = AC$,$AE$平分$\angle BAC$,根据等腰三角形三线合一,可得
$AE\perp BC$
,$BE = EC$。- 又因为$AC = AD$,$AF$是$CD$边上的中线,同理可得
$AF\perp CD$
,$CF = FD$。- 已知$BC = CD$,所以
$EC = CF$
。- 因为$PC\perp CD$,$QC\perp BC$,$\angle BCD=\angle BCD$,所以
$\angle PCE=\angle QCF$
。- 在$\triangle PCE$和$\triangle QCF$中,$\left\{\begin{array}{l}\angle PEC=\angle QFC = 90^{\circ}\\EC = FC\\\angle PCE=\angle QCF\end{array}\right.$,根据
$ASA$
可得$\triangle PCE\cong\triangle QCF$,所以$PC = QC$
。- 因为$AE\perp BC$,$QC\perp BC$,所以
$AE// QC$
;同理$AF// PC$
,所以四边形$APCQ$是平行四边形。- 又因为
$PC = QC$
,根据一组邻边相等的平行四边形是菱形,所以平行四边形$APCQ$是菱形。
答案:
【解析】:
- 因为$AB = AC$,$AE$平分$\angle BAC$,根据等腰三角形三线合一,可得$AE\perp BC$,$BE = EC$。
- 又因为$AC = AD$,$AF$是$CD$边上的中线,同理可得$AF\perp CD$,$CF = FD$。
- 已知$BC = CD$,所以$EC = CF$。
- 因为$PC\perp CD$,$QC\perp BC$,$\angle BCD=\angle BCD$,所以$\angle PCE=\angle QCF$。
- 在$\triangle PCE$和$\triangle QCF$中,$\left\{\begin{array}{l}\angle PEC=\angle QFC = 90^{\circ}\\EC = FC\\\angle PCE=\angle QCF\end{array}\right.$,根据$ASA$(角边角)可得$\triangle PCE\cong\triangle QCF$,所以$PC = QC$。
- 因为$AE\perp BC$,$QC\perp BC$,所以$AE// QC$;同理$AF// PC$,所以四边形$APCQ$是平行四边形。
- 又因为$PC = QC$,根据一组邻边相等的平行四边形是菱形,所以平行四边形$APCQ$是菱形。
【答案】:四边形$APCQ$是菱形。
- 因为$AB = AC$,$AE$平分$\angle BAC$,根据等腰三角形三线合一,可得$AE\perp BC$,$BE = EC$。
- 又因为$AC = AD$,$AF$是$CD$边上的中线,同理可得$AF\perp CD$,$CF = FD$。
- 已知$BC = CD$,所以$EC = CF$。
- 因为$PC\perp CD$,$QC\perp BC$,$\angle BCD=\angle BCD$,所以$\angle PCE=\angle QCF$。
- 在$\triangle PCE$和$\triangle QCF$中,$\left\{\begin{array}{l}\angle PEC=\angle QFC = 90^{\circ}\\EC = FC\\\angle PCE=\angle QCF\end{array}\right.$,根据$ASA$(角边角)可得$\triangle PCE\cong\triangle QCF$,所以$PC = QC$。
- 因为$AE\perp BC$,$QC\perp BC$,所以$AE// QC$;同理$AF// PC$,所以四边形$APCQ$是平行四边形。
- 又因为$PC = QC$,根据一组邻边相等的平行四边形是菱形,所以平行四边形$APCQ$是菱形。
【答案】:四边形$APCQ$是菱形。
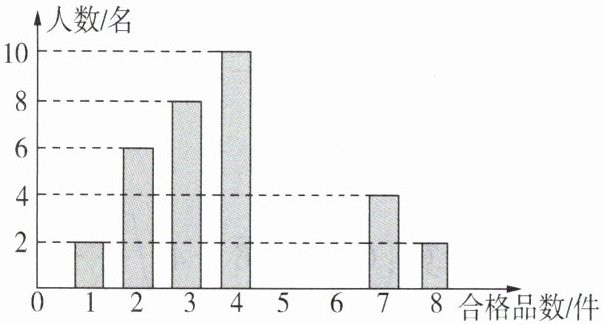
9. 某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了50名工人加工的零件进行检测,统计出他们各自加工的合格品数是1到8这八个整数,现提供统计图的部分信息如图所示.
请解答下列问题:
(1)根据统计图,求这50名工人加工出的合格品数的中位数.
(2)写出这50名工人加工出合格品数的众数的可能取值.
(3)厂方认定,工人在单位时间内加工出的合格品数不低于3件为技能合格,否则,将接受技能再培训.已知该厂有同类工人400名,请估计该厂将接受技能再培训的人数.
请解答下列问题:
(1)根据统计图,求这50名工人加工出的合格品数的中位数.
4
(2)写出这50名工人加工出合格品数的众数的可能取值.
4、5、6
(3)厂方认定,工人在单位时间内加工出的合格品数不低于3件为技能合格,否则,将接受技能再培训.已知该厂有同类工人400名,请估计该厂将接受技能再培训的人数.
64

答案:
【解析】:
### $(1)$求中位数
中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(如果数据个数是奇数),或者最中间两个数的平均数(如果数据个数是偶数)。
将合格品数从小到大排列,$50$是偶数,所以中位数是第$25$、$26$个数的平均数。
由统计图可知:合格品数为$1$的有$2$人,合格品数为$2$的有$6$人,合格品数为$3$的有$8$人,合格品数为$4$的有$10$人。
前$2 + 6+8 = 16$人,前$2 + 6+8 + 10=26$人,所以第$25$、$26$个数都是$4$,则中位数是$4$。
### $(2)$求众数的可能取值
众数是一组数据中出现次数最多的数据。
已知合格品数为$1$的有$2$人,合格品数为$2$的有$6$人,合格品数为$3$的有$8$人,合格品数为$4$的有$10$人,合格品数为$7$的有$4$人,合格品数为$8$的有$2$人,而合格品数为$5$、$6$的人数之和为$50-(2 + 6+8 + 10+4 + 2)=18$人。
若合格品数为$5$的人数$\geqslant10$人,则众数是$5$;
若合格品数为$6$的人数$\geqslant10$人,则众数是$6$;
若合格品数为$5$、$6$的人数都小于$10$人,则众数是$4$。
所以众数可能是$4$、$5$、$6$。
### $(3)$估计接受技能再培训的人数
先算出样本中加工合格品数低于$3$件(即$1$件和$2$件)的频率,再用总人数乘以该频率。
样本中加工合格品数低于$3$件的人数为$2 + 6=8$人,频率为$\frac{8}{50}$。
该厂有同类工人$400$名,所以接受技能再培训的人数约为$400×\frac{2 + 6}{50}=400×\frac{8}{50}=64$人。
【答案】:
$(1)$ $4$;
$(2)$ $4$、$5$、$6$;
$(3)$ $64$。
### $(1)$求中位数
中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(如果数据个数是奇数),或者最中间两个数的平均数(如果数据个数是偶数)。
将合格品数从小到大排列,$50$是偶数,所以中位数是第$25$、$26$个数的平均数。
由统计图可知:合格品数为$1$的有$2$人,合格品数为$2$的有$6$人,合格品数为$3$的有$8$人,合格品数为$4$的有$10$人。
前$2 + 6+8 = 16$人,前$2 + 6+8 + 10=26$人,所以第$25$、$26$个数都是$4$,则中位数是$4$。
### $(2)$求众数的可能取值
众数是一组数据中出现次数最多的数据。
已知合格品数为$1$的有$2$人,合格品数为$2$的有$6$人,合格品数为$3$的有$8$人,合格品数为$4$的有$10$人,合格品数为$7$的有$4$人,合格品数为$8$的有$2$人,而合格品数为$5$、$6$的人数之和为$50-(2 + 6+8 + 10+4 + 2)=18$人。
若合格品数为$5$的人数$\geqslant10$人,则众数是$5$;
若合格品数为$6$的人数$\geqslant10$人,则众数是$6$;
若合格品数为$5$、$6$的人数都小于$10$人,则众数是$4$。
所以众数可能是$4$、$5$、$6$。
### $(3)$估计接受技能再培训的人数
先算出样本中加工合格品数低于$3$件(即$1$件和$2$件)的频率,再用总人数乘以该频率。
样本中加工合格品数低于$3$件的人数为$2 + 6=8$人,频率为$\frac{8}{50}$。
该厂有同类工人$400$名,所以接受技能再培训的人数约为$400×\frac{2 + 6}{50}=400×\frac{8}{50}=64$人。
【答案】:
$(1)$ $4$;
$(2)$ $4$、$5$、$6$;
$(3)$ $64$。
查看更多完整答案,请扫码查看


