2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 一束阳光从窗户射入室内.如图所示,已知窗台A点离地面1米,光线与地面的交点B离墙2.4米,那么AB的长度是
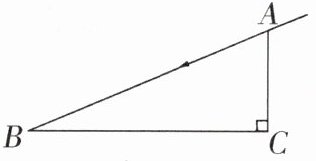
2.6米
?
答案:
【解析】:
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 1$米,$BC = 2.4$米。
根据勾股定理$AB^{2}=AC^{2}+BC^{2}$,则$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{1^{2}+2.4^{2}}=\sqrt{1 + 5.76}=\sqrt{6.76}=2.6$(米)。
【答案】:$2.6$米
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 1$米,$BC = 2.4$米。
根据勾股定理$AB^{2}=AC^{2}+BC^{2}$,则$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{1^{2}+2.4^{2}}=\sqrt{1 + 5.76}=\sqrt{6.76}=2.6$(米)。
【答案】:$2.6$米
9. 如图,点O是线段AB上的一点,OA= OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形.
(2)当∠AOC为
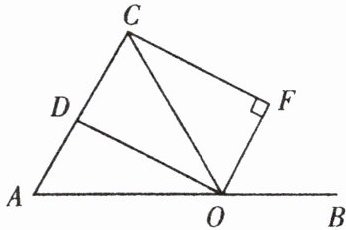
(1)求证:四边形CDOF是矩形.
(2)当∠AOC为
90°
时,四边形CDOF是正方形?并说明理由.
答案:
【解析】:
(1)
- 因为$OD$平分$\angle AOC$,$OF$平分$\angle COB$,$\angle AOC+\angle COB = 180^{\circ}$,所以$\angle DOF=\angle DOC+\angle COF=\frac{1}{2}\angle AOC+\frac{1}{2}\angle COB=\frac{1}{2}(\angle AOC + \angle COB)=90^{\circ}$。
- 因为$OA = OC$,$OD$平分$\angle AOC$,根据等腰三角形三线合一,$OD\perp AC$,即$\angle CDO = 90^{\circ}$。
- 又因为$CF\perp OF$,即$\angle F = 90^{\circ}$。
- 四个角都是直角的四边形是矩形,所以四边形$CDOF$是矩形。
(2)
- 当$\angle AOC = 90^{\circ}$时。
- 因为$OA = OC$,$\angle AOC = 90^{\circ}$,$OD$平分$\angle AOC$,根据等腰直角三角形三线合一,$OD = CD=\frac{1}{2}AC$。
- 由
(1)知四边形$CDOF$是矩形,一组邻边相等的矩形是正方形,此时$CD = OD$,所以四边形$CDOF$是正方形。
【答案】:
(1) 证明见上述解析。
(2) 当$\angle AOC = 90^{\circ}$时,四边形$CDOF$是正方形,理由见上述解析。
(1)
- 因为$OD$平分$\angle AOC$,$OF$平分$\angle COB$,$\angle AOC+\angle COB = 180^{\circ}$,所以$\angle DOF=\angle DOC+\angle COF=\frac{1}{2}\angle AOC+\frac{1}{2}\angle COB=\frac{1}{2}(\angle AOC + \angle COB)=90^{\circ}$。
- 因为$OA = OC$,$OD$平分$\angle AOC$,根据等腰三角形三线合一,$OD\perp AC$,即$\angle CDO = 90^{\circ}$。
- 又因为$CF\perp OF$,即$\angle F = 90^{\circ}$。
- 四个角都是直角的四边形是矩形,所以四边形$CDOF$是矩形。
(2)
- 当$\angle AOC = 90^{\circ}$时。
- 因为$OA = OC$,$\angle AOC = 90^{\circ}$,$OD$平分$\angle AOC$,根据等腰直角三角形三线合一,$OD = CD=\frac{1}{2}AC$。
- 由
(1)知四边形$CDOF$是矩形,一组邻边相等的矩形是正方形,此时$CD = OD$,所以四边形$CDOF$是正方形。
【答案】:
(1) 证明见上述解析。
(2) 当$\angle AOC = 90^{\circ}$时,四边形$CDOF$是正方形,理由见上述解析。
10. 甲、乙两人参加某项体育训练,近5次的测试成绩情况如图所示:
(1)分别求出两人得分的平均数与方差;
甲的平均数为
(2)根据图象和上面算得的结果,对两人的训练成绩作出评价.
甲、乙平均成绩相同,乙的成绩更稳定,甲的成绩在不断提高,乙的成绩无明显提高。
(1)分别求出两人得分的平均数与方差;
甲的平均数为
13
,方差为4
;乙的平均数为13
,方差为0.8
。(2)根据图象和上面算得的结果,对两人的训练成绩作出评价.
甲、乙平均成绩相同,乙的成绩更稳定,甲的成绩在不断提高,乙的成绩无明显提高。
答案:
【解析】:
### $(1)$计算两人得分的平均数与方差
**计算甲得分的平均数$\overline{x}_{甲}$:**
根据平均数公式$\overline{x}=\frac{1}{n}(x_{1}+x_{2}+\cdots +x_{n})$(其中$n = 5$,$x_{i}$为第$i$次成绩),甲的成绩分别为$10$,$13$,$12$,$14$,$16$,则$\overline{x}_{甲}=\frac{10 + 13 + 12 + 14 + 16}{5}=\frac{65}{5}=13$。
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\cdots+(x_{n}-\overline{x})^{2}]$,可得:
$\begin{aligned}s_{甲}^{2}&=\frac{1}{5}[(10 - 13)^{2}+(13 - 13)^{2}+(12 - 13)^{2}+(14 - 13)^{2}+(16 - 13)^{2}]\\&=\frac{1}{5}[(-3)^{2}+0^{2}+(-1)^{2}+1^{2}+3^{2}]\\&=\frac{1}{5}(9 + 0+1 + 1+9)\\&=\frac{20}{5}\\&= 4\end{aligned}$
**计算乙得分的平均数$\overline{x}_{乙}$:**
乙的成绩分别为$13$,$14$,$12$,$12$,$14$,则$\overline{x}_{乙}=\frac{13 + 14 + 12 + 12 + 14}{5}=\frac{65}{5}=13$。
根据方差公式,可得:
$\begin{aligned}s_{乙}^{2}&=\frac{1}{5}[(13 - 13)^{2}+(14 - 13)^{2}+(12 - 13)^{2}+(12 - 13)^{2}+(14 - 13)^{2}]\\&=\frac{1}{5}[0^{2}+1^{2}+(-1)^{2}+(-1)^{2}+1^{2}]\\&=\frac{1}{5}(0 + 1+1 + 1+1)\\&=\frac{4}{5}\\&= 0.8\end{aligned}$
### $(2)$对两人的训练成绩作出评价
因为$\overline{x}_{甲}=\overline{x}_{乙}=13$,说明甲、乙两人的平均成绩相同。
又因为$s_{甲}^{2}=4\gt s_{乙}^{2}=0.8$,方差越大,表明这组数据波动越大,所以乙的成绩比甲的成绩更稳定。
从折线图看,甲的成绩基本上呈上升状态,而乙的成绩在平均线上下波动, 所以甲的成绩在不断提高,而乙的成绩则无明显提高。
【答案】:
$(1)$$\boldsymbol{\overline{x}_{甲}=13}$,$\boldsymbol{s_{甲}^{2}=4}$;$\boldsymbol{\overline{x}_{乙}=13}$,$\boldsymbol{s_{乙}^{2}=0.8}$。
$(2)$甲、乙平均成绩相同,乙的成绩更稳定,甲的成绩在不断提高,乙的成绩无明显提高。
### $(1)$计算两人得分的平均数与方差
**计算甲得分的平均数$\overline{x}_{甲}$:**
根据平均数公式$\overline{x}=\frac{1}{n}(x_{1}+x_{2}+\cdots +x_{n})$(其中$n = 5$,$x_{i}$为第$i$次成绩),甲的成绩分别为$10$,$13$,$12$,$14$,$16$,则$\overline{x}_{甲}=\frac{10 + 13 + 12 + 14 + 16}{5}=\frac{65}{5}=13$。
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\cdots+(x_{n}-\overline{x})^{2}]$,可得:
$\begin{aligned}s_{甲}^{2}&=\frac{1}{5}[(10 - 13)^{2}+(13 - 13)^{2}+(12 - 13)^{2}+(14 - 13)^{2}+(16 - 13)^{2}]\\&=\frac{1}{5}[(-3)^{2}+0^{2}+(-1)^{2}+1^{2}+3^{2}]\\&=\frac{1}{5}(9 + 0+1 + 1+9)\\&=\frac{20}{5}\\&= 4\end{aligned}$
**计算乙得分的平均数$\overline{x}_{乙}$:**
乙的成绩分别为$13$,$14$,$12$,$12$,$14$,则$\overline{x}_{乙}=\frac{13 + 14 + 12 + 12 + 14}{5}=\frac{65}{5}=13$。
根据方差公式,可得:
$\begin{aligned}s_{乙}^{2}&=\frac{1}{5}[(13 - 13)^{2}+(14 - 13)^{2}+(12 - 13)^{2}+(12 - 13)^{2}+(14 - 13)^{2}]\\&=\frac{1}{5}[0^{2}+1^{2}+(-1)^{2}+(-1)^{2}+1^{2}]\\&=\frac{1}{5}(0 + 1+1 + 1+1)\\&=\frac{4}{5}\\&= 0.8\end{aligned}$
### $(2)$对两人的训练成绩作出评价
因为$\overline{x}_{甲}=\overline{x}_{乙}=13$,说明甲、乙两人的平均成绩相同。
又因为$s_{甲}^{2}=4\gt s_{乙}^{2}=0.8$,方差越大,表明这组数据波动越大,所以乙的成绩比甲的成绩更稳定。
从折线图看,甲的成绩基本上呈上升状态,而乙的成绩在平均线上下波动, 所以甲的成绩在不断提高,而乙的成绩则无明显提高。
【答案】:
$(1)$$\boldsymbol{\overline{x}_{甲}=13}$,$\boldsymbol{s_{甲}^{2}=4}$;$\boldsymbol{\overline{x}_{乙}=13}$,$\boldsymbol{s_{乙}^{2}=0.8}$。
$(2)$甲、乙平均成绩相同,乙的成绩更稳定,甲的成绩在不断提高,乙的成绩无明显提高。
查看更多完整答案,请扫码查看


