2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 已知:如图,在$\triangle ABC$中,$CD是AB$边上的高,且$CD^{2}= AD\cdot BD$.
求证:$\triangle ABC$是直角三角形.
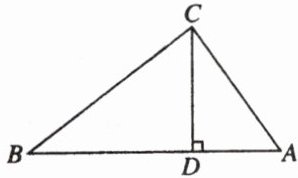
证明:因为$CD$是$AB$边上的高,所以$\angle BDC = \angle CDA = 90^{\circ}$。
在$Rt\triangle BCD$中,根据勾股定理可得$BC^{2}=$
所以$BC^{2}+AC^{2}=$
又因为$CD^{2}=AD\cdot BD$,则$BC^{2}+AC^{2}=$
对$AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}$进行变形可得:
$\begin{aligned}&AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}\\=&BD(AD + BD)+AD(AD + BD)\\=&(AD + BD)(AD + BD)\\=&AB^{2}\end{aligned}$
即$BC^{2}+AC^{2}=$
根据勾股定理的逆定理,如果一个三角形的三边$a$、$b$、$c$满足$a^{2}+b^{2}=c^{2}$,那么这个三角形是直角三角形,其中$c$为斜边。
在$\triangle ABC$中,$BC^{2}+AC^{2}=AB^{2}$,所以$\triangle ABC$是直角三角形。
求证:$\triangle ABC$是直角三角形.

证明:因为$CD$是$AB$边上的高,所以$\angle BDC = \angle CDA = 90^{\circ}$。
在$Rt\triangle BCD$中,根据勾股定理可得$BC^{2}=$
$CD^{2}+BD^{2}$
;在$Rt\triangle ACD$中,根据勾股定理可得$AC^{2}=$$CD^{2}+AD^{2}$
。所以$BC^{2}+AC^{2}=$
$CD^{2}+BD^{2}+CD^{2}+AD^{2}$
。又因为$CD^{2}=AD\cdot BD$,则$BC^{2}+AC^{2}=$
$AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}$
。对$AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}$进行变形可得:
$\begin{aligned}&AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}\\=&BD(AD + BD)+AD(AD + BD)\\=&(AD + BD)(AD + BD)\\=&AB^{2}\end{aligned}$
即$BC^{2}+AC^{2}=$
$AB^{2}$
。根据勾股定理的逆定理,如果一个三角形的三边$a$、$b$、$c$满足$a^{2}+b^{2}=c^{2}$,那么这个三角形是直角三角形,其中$c$为斜边。
在$\triangle ABC$中,$BC^{2}+AC^{2}=AB^{2}$,所以$\triangle ABC$是直角三角形。
答案:
【解析】:
因为$CD$是$AB$边上的高,所以$\angle BDC = \angle CDA = 90^{\circ}$。
在$Rt\triangle BCD$中,根据勾股定理可得$BC^{2}=CD^{2}+BD^{2}$;在$Rt\triangle ACD$中,根据勾股定理可得$AC^{2}=CD^{2}+AD^{2}$。
所以$BC^{2}+AC^{2}=CD^{2}+BD^{2}+CD^{2}+AD^{2}$。
又因为$CD^{2}=AD\cdot BD$,则$BC^{2}+AC^{2}=AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}$。
对$AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}$进行变形可得:
$\begin{aligned}&AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}\\=&BD(AD + BD)+AD(AD + BD)\\=&(AD + BD)(AD + BD)\\=&AB^{2}\end{aligned}$
即$BC^{2}+AC^{2}=AB^{2}$。
根据勾股定理的逆定理,如果一个三角形的三边$a$、$b$、$c$满足$a^{2}+b^{2}=c^{2}$,那么这个三角形是直角三角形,其中$c$为斜边。
在$\triangle ABC$中,$BC^{2}+AC^{2}=AB^{2}$,所以$\triangle ABC$是直角三角形。
【答案】:$\triangle ABC$是直角三角形。
因为$CD$是$AB$边上的高,所以$\angle BDC = \angle CDA = 90^{\circ}$。
在$Rt\triangle BCD$中,根据勾股定理可得$BC^{2}=CD^{2}+BD^{2}$;在$Rt\triangle ACD$中,根据勾股定理可得$AC^{2}=CD^{2}+AD^{2}$。
所以$BC^{2}+AC^{2}=CD^{2}+BD^{2}+CD^{2}+AD^{2}$。
又因为$CD^{2}=AD\cdot BD$,则$BC^{2}+AC^{2}=AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}$。
对$AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}$进行变形可得:
$\begin{aligned}&AD\cdot BD + BD^{2}+AD\cdot BD+AD^{2}\\=&BD(AD + BD)+AD(AD + BD)\\=&(AD + BD)(AD + BD)\\=&AB^{2}\end{aligned}$
即$BC^{2}+AC^{2}=AB^{2}$。
根据勾股定理的逆定理,如果一个三角形的三边$a$、$b$、$c$满足$a^{2}+b^{2}=c^{2}$,那么这个三角形是直角三角形,其中$c$为斜边。
在$\triangle ABC$中,$BC^{2}+AC^{2}=AB^{2}$,所以$\triangle ABC$是直角三角形。
【答案】:$\triangle ABC$是直角三角形。
9. 某风景区集体门票的收费标准是 20 人以内(含 20 人)每人 25 元,若超过 20 人,超过部分每人 10 元.
(1)写出应收门票$y$(元)与游览人数$x$(人)之间的函数关系式;
(2)利用(1)中函数关系式计算某班 54 名学生去该风景区游览时,购门票共花了多少元.
(1)写出应收门票$y$(元)与游览人数$x$(人)之间的函数关系式;
(2)利用(1)中函数关系式计算某班 54 名学生去该风景区游览时,购门票共花了多少元.
答案:
【解析】:
1. 首先分析应收门票$y$(元)与游览人数$x$(人)之间的函数关系式:
当$0\lt x\leqslant20$时:
因为$20$人以内(含$20$人)每人$25$元,根据“总价 = 单价×数量”,此时$y = 25x$。
当$x\gt20$时:
前$20$人的门票费用为$20×25 = 500$元。
超过$20$人的人数为$(x - 20)$人,超过部分每人$10$元,则超过$20$人部分的门票费用为$10(x - 20)$元。
那么总门票费用$y=20×25 + 10(x - 20)$,化简可得$y = 500+10x - 200=10x + 300$。
综上,函数关系式为$y=\begin{cases}25x(0\lt x\leqslant20)\\10x + 300(x\gt20)\end{cases}$。
2. 然后计算某班$54$名学生去该风景区游览时的门票费用:
因为$x = 54\gt20$,所以将$x = 54$代入$y = 10x+300$中。
则$y=10×54 + 300$。
先计算乘法:$10×54 = 540$,再计算加法:$540+300 = 840$(元)。
【答案】:
(1)$y=\begin{cases}25x(0\lt x\leqslant20)\\10x + 300(x\gt20)\end{cases}$;
(2)$840$元
1. 首先分析应收门票$y$(元)与游览人数$x$(人)之间的函数关系式:
当$0\lt x\leqslant20$时:
因为$20$人以内(含$20$人)每人$25$元,根据“总价 = 单价×数量”,此时$y = 25x$。
当$x\gt20$时:
前$20$人的门票费用为$20×25 = 500$元。
超过$20$人的人数为$(x - 20)$人,超过部分每人$10$元,则超过$20$人部分的门票费用为$10(x - 20)$元。
那么总门票费用$y=20×25 + 10(x - 20)$,化简可得$y = 500+10x - 200=10x + 300$。
综上,函数关系式为$y=\begin{cases}25x(0\lt x\leqslant20)\\10x + 300(x\gt20)\end{cases}$。
2. 然后计算某班$54$名学生去该风景区游览时的门票费用:
因为$x = 54\gt20$,所以将$x = 54$代入$y = 10x+300$中。
则$y=10×54 + 300$。
先计算乘法:$10×54 = 540$,再计算加法:$540+300 = 840$(元)。
【答案】:
(1)$y=\begin{cases}25x(0\lt x\leqslant20)\\10x + 300(x\gt20)\end{cases}$;
(2)$840$元
查看更多完整答案,请扫码查看


