《2025年假期园地暑假作业八年级数学人教版》

1. 下列各式中,一定是二次根式的是(B)
A.$\sqrt { - 9 }$
B.$\sqrt { 2 a }$
C.$x ^ { 2 } + 4$
D.$x - 1$

答案： B

2. 下列二次根式中,最简二次根式是(B)
A.$\sqrt { 16 a }$
B.$\sqrt { x ^ { 2 } - 9 }$
C.$\sqrt { \frac { x + y } { x } }$
D.$\sqrt { 3 x ^ { 2 } }$

答案： B

3. 要使式子$\sqrt { 1 - 3 x }$有意义,则$x$的取值范围是(D)
A.$x \geq \frac { 1 } { 3 }$
B.$x ＞ \frac { 1 } { 3 }$
C.$x ＜ \frac { 1 } { 3 }$
D.$x \leq \frac { 1 } { 3 }$

答案： D

4. 请写出一个图象经过第一、三象限的正比例函数的解析式$y = 2x$（答案不唯一）.

答案： $y = 2x$（答案不唯一）

5. 计算：$\frac { \sqrt { 3 } + 1 } { \sqrt { 3 } - 1 } - ( 3 \sqrt { 2 } - 2 \sqrt { 3 } ) ( 3 \sqrt { 2 } + 2 \sqrt { 3 } ) = $$\sqrt{3} - 4$.

答案： $\sqrt{3} - 4$

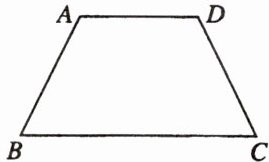
6. 如图,在四边形$ABCD$中,$AD // BC$,$AD = 4$,$AB = CD = 5$,$\angle B = 60 ^ { \circ }$,则下底$BC$的长为______9.

答案： $9$

7. 先化简,再求值：
$( \frac { a ^ { 2 } - 5 a + 2 } { a + 2 } + 1 ) ÷ \frac { a ^ { 2 } - 4 } { a ^ { 2 } + 4 a + 4 }$,其中$a = 2 + \sqrt { 3 }$.

答案： 【解析】：
本题可先对原式进行化简，再将$a = 2 + \sqrt { 3 }$代入化简后的式子求值。
- **步骤一：化简原式**
**化简$(\frac{a^2 - 5a + 2}{a + 2} + 1)$：**
对$(\frac{a^2 - 5a + 2}{a + 2} + 1)$进行通分，可得$\frac{a^2 - 5a + 2}{a + 2} + \frac{a + 2}{a + 2}$，根据同分母分式的加法法则：同分母的分式相加，分母不变，分子相加，可得$\frac{a^2 - 5a + 2 + a + 2}{a + 2}=\frac{a^2 - 4a + 4}{a + 2}$。
根据完全平方公式$(m-n)^2=m^2-2mn+n^2$，对分子$a^2 - 4a + 4$进行因式分解，可得$\frac{(a - 2)^2}{a + 2}$。
**化简$\frac{a^2 - 4}{a^2 + 4a + 4}$：**
根据平方差公式$m^2-n^2=(m+n)(m-n)$，对分子$a^2 - 4$进行因式分解，可得$a^2 - 4=(a + 2)(a - 2)$。
根据完全平方公式$(m+n)^2=m^2+2mn+n^2$，对分母$a^2 + 4a + 4$进行因式分解，可得$a^2 + 4a + 4=(a + 2)^2$。
所以$\frac{a^2 - 4}{a^2 + 4a + 4}=\frac{(a + 2)(a - 2)}{(a + 2)^2}=\frac{a - 2}{a + 2}$。
**计算$(\frac{a^2 - 5a + 2}{a + 2} + 1)÷\frac{a^2 - 4}{a^2 + 4a + 4}$：**
根据除法运算法则，除以一个数等于乘以它的倒数，则$(\frac{a^2 - 5a + 2}{a + 2} + 1)÷\frac{a^2 - 4}{a^2 + 4a + 4}=\frac{(a - 2)^2}{a + 2}×\frac{a + 2}{a - 2}$，约分可得$a - 2$。
- **步骤二：代入求值**
将$a = 2 + \sqrt { 3 }$代入$a - 2$，可得$2 + \sqrt { 3 } - 2=\sqrt { 3 }$。
【答案】：$\sqrt { 3 }$