《2025年假期园地暑假作业八年级数学人教版》

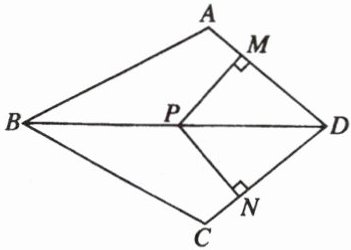
8. 如图,在四边形$ABCD$中,$AB = BC$,对角线$BD$平分$\angle ABC$,$P是BD$上一点,过点$P作PM \perp AD$,$PN \perp CD$,垂足分别为$M$,$N$.
(1) 求证：$\angle ADB = \angle CDB$；
证明：因为$BD$平分$\angle ABC$，所以$\angle ABD=\angle CBD$。又因为$AB = BC$，$BD = BD$（公共边），根据$SAS$（边角边）定理可得$\triangle ABD\cong\triangle CBD$。根据全等三角形的性质，全等三角形对应角相等，所以$\angle ADB=\angle CDB$。
(2) 若$\angle ADC = 90 ^ { \circ }$,求证：四边形$MPND$是正方形.
证明：因为$PM\perp AD$，$PN\perp CD$，$\angle ADC = 90^{\circ}$，即$\angle PMD=\angle PND=\angle ADC = 90^{\circ}$。所以四边形$MPND$是矩形（有三个角是直角的四边形是矩形）。又因为$\angle ADB=\angle CDB$，$PM\perp AD$，$PN\perp CD$，根据角平分线的性质：角平分线上的点到角两边的距离相等，可得$PM = PN$。一组邻边相等的矩形是正方形，所以四边形$MPND$是正方形。

答案： 【解析】：
(1) 因为$BD$平分$\angle ABC$，所以$\angle ABD=\angle CBD$。
又因为$AB = BC$，$BD = BD$（公共边），根据$SAS$（边角边）定理可得$\triangle ABD\cong\triangle CBD$。
根据全等三角形的性质，全等三角形对应角相等，所以$\angle ADB=\angle CDB$。
(2) 因为$PM\perp AD$，$PN\perp CD$，$\angle ADC = 90^{\circ}$，即$\angle PMD=\angle PND=\angle ADC = 90^{\circ}$。
所以四边形$MPND$是矩形（有三个角是直角的四边形是矩形）。
又因为$\angle ADB=\angle CDB$，$PM\perp AD$，$PN\perp CD$，根据角平分线的性质：角平分线上的点到角两边的距离相等，可得$PM = PN$。
一组邻边相等的矩形是正方形，所以四边形$MPND$是正方形。
【答案】：
(1) 证明见上述解析；
(2) 证明见上述解析。

9. 甲地至乙地高速公路的路基工程分段招标,某路桥公司中标承包了一段路基工程,进入施工场地后,所挖筑路基的长度$y ( \mathrm { m } )与挖筑时间x$(天)之间的函数关系如图所示. 请根据图象提供的信息,解答下面的问题：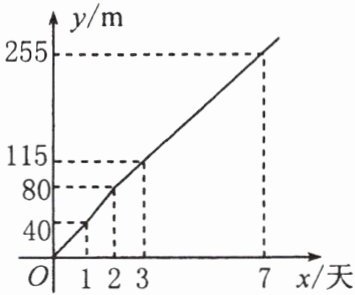
(1) 求：①在$0 \leq x ＜ 2$的时间段内,$y与x$之间的函数解析式；$y = 40x$
②在$x \geq 2$的时间段内,$y与x$之间的函数解析式.$y = 35x + 10$
(2) 预测完成$1620 \mathrm { m }$的路基工程,需要挖筑多少天？46天

答案： 【解析】：
### （1）求函数解析式
**①在$0\leq x\lt2$的时间段内：**
设$y$与$x$之间的函数解析式为$y = kx(k\neq0)$。
因为图象过点$(1,40)$，将$x = 1$，$y = 40$代入$y = kx$中，可得$40=k×1$，解得$k = 40$。
所以在$0\leq x\lt2$的时间段内，$y$与$x$之间的函数解析式为$y = 40x$。
**②在$x\geq2$的时间段内：**
设$y$与$x$之间的函数解析式为$y=ax + b(a\neq0)$。
因为图象过点$(2,80)$，$(3,115)$，将其代入$y = ax + b$中，得到方程组$\begin{cases}2a + b = 80\\3a + b = 115\end{cases}$。
用$3a + b = 115$减去$2a + b = 80$，可得：
$(3a + b)-(2a + b)=115 - 80$
$3a + b - 2a - b = 35$
$a = 35$。
把$a = 35$代入$2a + b = 80$，得$2×35 + b = 80$，$70 + b = 80$，解得$b = 10$。
所以在$x\geq2$的时间段内，$y$与$x$之间的函数解析式为$y = 35x + 10$。
### （2）预测完成$1620m$的路基工程所需天数
当$y = 1620$时，因为$1620\gt80$（$x = 2$时，$y = 80$），所以把$y = 1620$代入$y = 35x + 10$中，得到$1620 = 35x + 10$。
移项可得$35x=1620 - 10$，即$35x = 1610$。
解得$x = 46$。
【答案】：
(1) ①$y = 40x$；②$y = 35x + 10$
(2)$46$天