《2025年假期园地暑假作业八年级数学人教版》

7. 先化简,再求值：
$ 2 ( a - \sqrt { 3 } ) ( a + \sqrt { 3 } ) - a ( a - 6 ) + 6 $,其中 $ a = \sqrt { 2 } - 1 $。

答案： 【解析】：
本题可先根据平方差公式和单项式乘多项式的运算法则对原式进行化简，再将$a = \sqrt { 2 } - 1$代入化简后的式子求值。
- **步骤一：化简原式**
**利用平方差公式化简$2(a - \sqrt { 3 })(a + \sqrt { 3 })$：**
平方差公式为$(m-n)(m+n)=m^2-n^2$，在$2(a - \sqrt { 3 })(a + \sqrt { 3 })$中，$m = a$，$n = \sqrt{3}$，则$2(a - \sqrt { 3 })(a + \sqrt { 3 })=2(a^2 - (\sqrt{3})^2)=2(a^2 - 3)=2a^2 - 6$。
**利用单项式乘多项式的运算法则化简$a(a - 6)$：**
单项式乘多项式的运算法则为$m(n+p)=mn+mp$，在$a(a - 6)$中，$m = a$，$n = a$，$p = -6$，则$a(a - 6)=a^2 - 6a$。
**将上述化简结果代入原式并合并同类项：**
$\begin{aligned}&2 ( a - \sqrt { 3 } ) ( a + \sqrt { 3 } ) - a ( a - 6 ) + 6\\=&2a^2 - 6 - (a^2 - 6a) + 6\\=&2a^2 - 6 - a^2 + 6a + 6\\=&(2a^2 - a^2) + 6a + (- 6 + 6)\\=&a^2 + 6a\end{aligned}$
- **步骤二：代入求值**
将$a = \sqrt { 2 } - 1$代入$a^2 + 6a$可得：
$\begin{aligned}&(\sqrt { 2 } - 1)^2 + 6(\sqrt { 2 } - 1)\\=&(\sqrt{2})^2 - 2\sqrt{2} + 1^2 + 6\sqrt{2} - 6\\=&2 - 2\sqrt{2} + 1 + 6\sqrt{2} - 6\\=&(2 + 1 - 6) + (- 2\sqrt{2} + 6\sqrt{2})\\=& -3 + 4\sqrt{2}\end{aligned}$
【答案】：$-3 + 4\sqrt{2}$

8. 如图,在 $ \triangle ABC $ 中,$ D $,$ E $,$ F $ 分别为边 $ AB $,$ BC $,$ CA $ 的中点。求证：四边形 $ DECF $ 是平行四边形。
证明：因为$D$，$F$分别为边$AB$，$CA$的中点，所以$DF// BC$（三角形中位线定理），即$DF// EC$；
因为$E$，$F$分别为边$BC$，$CA$的中点，所以$EF// AB$（三角形中位线定理），即$EF// DC$；
所以四边形$DECF$是平行四边形（两组对边分别平行的四边形是平行四边形）。

答案： 【解析】：
- 因为$D$，$F$分别为边$AB$，$CA$的中点，根据三角形中位线定理，可得$DF// BC$，即$DF// EC$。
- 又因为$E$，$F$分别为边$BC$，$CA$的中点，同理可得$EF// AB$，即$EF// DC$。
- 两组对边分别平行的四边形是平行四边形，所以四边形$DECF$是平行四边形。
【答案】：
因为$D$，$F$分别为边$AB$，$CA$的中点，所以$DF// BC$（三角形中位线定理），即$DF// EC$；
因为$E$，$F$分别为边$BC$，$CA$的中点，所以$EF// AB$（三角形中位线定理），即$EF// DC$；
所以四边形$DECF$是平行四边形（两组对边分别平行的四边形是平行四边形）。

9. 如图所示,在平面直角坐标系中,点 $ A $,$ B $ 的坐标分别为 $ ( - 3, 0 ) $,$ ( 0, 3 ) $。一次函数图象上的两点 $ P $,$ Q $ 在直线 $ AB $ 的同侧,且直线 $ PQ $ 与 $ y $ 轴交点在 $ y $ 轴正半轴上,若 $ \triangle QAB $ 和 $ \triangle PAB $ 的面积都等于 $ 3 $,求这个一次函数的解析式。

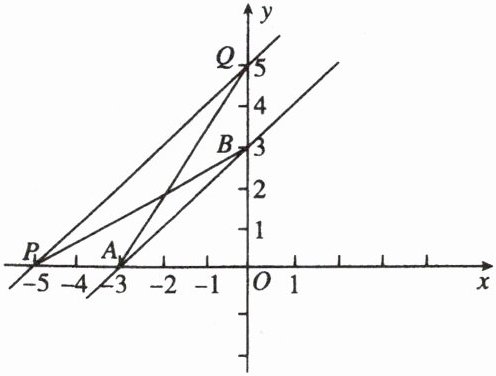
这个一次函数的解析式为$y = x + 5$。

答案： 【解析】：
1. 首先求直线$AB$的解析式：
设直线$AB$的解析式为$y = kx + b$，把$A(-3,0)$，$B(0,3)$代入可得$\begin{cases}-3k + b = 0\\b = 3\end{cases}$，解得$\begin{cases}k = 1\\b = 3\end{cases}$，所以直线$AB$的解析式为$y = x + 3$。
由$A(-3,0)$，$B(0,3)$可得$OA = 3$，$OB = 3$，根据勾股定理$AB=\sqrt{(-3 - 0)^2+(0 - 3)^2}=3\sqrt{2}$。
因为${S}_{\triangle PAB} = 3$，${S}_{\triangle QAB}=3$，且$A(-3,0)$，$B(0,3)$，根据三角形面积公式$S=\frac{1}{2}×底×高$，以$AB$为底，设$P$，$Q$到直线$AB$的距离为$h$，则$\frac{1}{2}× AB× h = 3$，$\frac{1}{2}×3\sqrt{2}× h = 3$，解得$h=\sqrt{2}$。
设与直线$AB$平行的直线$l$的解析式为$y=x + m$（两平行直线$y = k_1x + b_1$，$y = k_2x + b_2$，$k_1 = k_2$），根据两平行直线$Ax+By + C_1 = 0$，$Ax+By + C_2 = 0$间的距离公式$d=\frac{\vert C_1 - C_2\vert}{\sqrt{A^2 + B^2}}$，直线$AB$：$x - y+3 = 0$，直线$l$：$x - y+m = 0$，则$\frac{\vert m - 3\vert}{\sqrt{1^2+( - 1)^2}}=\sqrt{2}$，即$\vert m - 3\vert = 2$，解得$m = 1$或$m = 5$。
因为直线$PQ$与$y$轴交点在$y$轴正半轴上且$P$，$Q$在直线$AB$同侧，所以$m = 5$。
设直线$PQ$的解析式为$y=x + 5$，设$P(x_1,0)$，$Q(0,y_2)$。
因为${S}_{\triangle PAB}=\frac{1}{2}×\vert PA\vert×3 = 3$，$\vert PA\vert = 2$，又$A(-3,0)$，所以$P(-5,0)$；因为${S}_{\triangle QAB}=\frac{1}{2}×\vert QB\vert×3 = 3$，$\vert QB\vert = 2$，又$B(0,3)$，所以$Q(0,5)$。
设一次函数解析式为$y = kx + n$，把$P(-5,0)$，$Q(0,5)$代入可得$\begin{cases}-5k + n = 0\\n = 5\end{cases}$，解得$\begin{cases}k = 1\\n = 5\end{cases}$。
【答案】：$y = x + 5$