2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图所示,强台风“麦莎”过后,一棵大树在离地面3.6m处折断倒下,倒下部分与地面的接触点离树的底部为4.8m,则该树的原高度为(
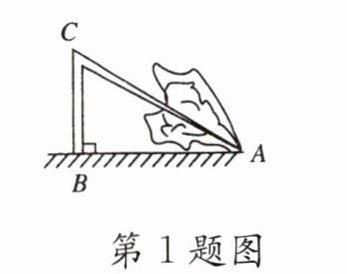
A.6m
B.8.4m
C.6.8m
D.9.6m
D
)
A.6m
B.8.4m
C.6.8m
D.9.6m
答案:
D
2. 放学以后,萍萍和晓晓从学校分手,分别沿东南方向和西南方向回家,若萍萍和晓晓行走的速度都是40m/min,萍萍用15min到家,晓晓用20min到家,萍萍家和晓晓家的距离为(
A.600m
B.800m
C.1000m
D.不能确定
C
)A.600m
B.800m
C.1000m
D.不能确定
答案:
C
3. 如图所示,一架25dm的梯子,斜立在一竖直的墙上,这时梯子距墙底端7dm,如果梯子的顶端沿墙下滑4dm,那么梯子将平滑(
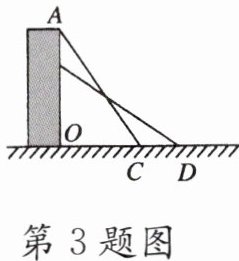
A.9dm
B.15dm
C.5dm
D.8dm
D
)
A.9dm
B.15dm
C.5dm
D.8dm
答案:
D
4. 在矩形ABCD中,两条对角线AC,BD相交于点O,若AB= OB= 4,则AD=
$4\sqrt{3}$
.
答案:
$4\sqrt{3}$
5. 在△ABC中,点D,E,F分别是AB,BC,CA的中点,若△ABC的周长为10cm,则△DEF的周长是
5
cm.
答案:
$5$
6. 在□ABCD中,对角线AC,BD相交于点O,若AC= 14,BD= 8,AB= 10,则△OAB的周长为______
21
.
答案:
$21$
7. 一次函数y= kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
答案:
【解析】:本题需要分$k\gt0$和$k\lt0$两种情况进行讨论。
- **当$k\gt0$时:**
一次函数$y = kx + b$中$y$随$x$的增大而增大。
已知自变量的取值范围是$-3\leq x\leq6$,相应函数值的取值范围是$-5\leq y\leq - 2$,所以当$x = - 3$时,$y = - 5$;当$x = 6$时,$y = - 2$。
将$\begin{cases}x = - 3\\y = - 5\end{cases}$和$\begin{cases}x = 6\\y = - 2\end{cases}$分别代入$y = kx + b$中,得到方程组$\begin{cases}-3k + b = - 5\\6k + b = - 2\end{cases}$。
用第二个方程$6k + b = - 2$减去第一个方程$-3k + b = - 5$,可得:
$\begin{aligned}(6k + b) - (-3k + b)&=-2 - (-5)\\6k + b + 3k - b&=-2 + 5\\9k&=3\\k&=\frac{1}{3}\end{aligned}$
把$k = \frac{1}{3}$代入$-3k + b = - 5$,可得:
$\begin{aligned}-3×\frac{1}{3} + b&=- 5\\-1 + b&=- 5\\b&=- 5 + 1\\b&=- 4\end{aligned}$
此时函数解析式为$y = \frac{1}{3}x - 4$。
- **当$k\lt0$时:**
一次函数$y = kx + b$中$y$随$x$的增大而减小。
已知自变量的取值范围是$-3\leq x\leq6$,相应函数值的取值范围是$-5\leq y\leq - 2$,所以当$x = - 3$时,$y = - 2$;当$x = 6$时,$y = - 5$。
将$\begin{cases}x = - 3\\y = - 2\end{cases}$和$\begin{cases}x = 6\\y = - 5\end{cases}$分别代入$y = kx + b$中,得到方程组$\begin{cases}-3k + b = - 2\\6k + b = - 5\end{cases}$。
用第二个方程$6k + b = - 5$减去第一个方程$-3k + b = - 2$,可得:
$\begin{aligned}(6k + b) - (-3k + b)&=-5 - (-2)\\6k + b + 3k - b&=-5 + 2\\9k&=-3\\k&=-\frac{1}{3}\end{aligned}$
把$k = -\frac{1}{3}$代入$-3k + b = - 2$,可得:
$\begin{aligned}-3×(-\frac{1}{3}) + b&=- 2\\1 + b&=- 2\\b&=- 2 - 1\\b&=- 3\end{aligned}$
此时函数解析式为$y = -\frac{1}{3}x - 3$。
综上,这个函数的解析式为$y = \frac{1}{3}x - 4$或$y = -\frac{1}{3}x - 3$。
【答案】:$y = \frac{1}{3}x - 4$或$y = -\frac{1}{3}x - 3$
- **当$k\gt0$时:**
一次函数$y = kx + b$中$y$随$x$的增大而增大。
已知自变量的取值范围是$-3\leq x\leq6$,相应函数值的取值范围是$-5\leq y\leq - 2$,所以当$x = - 3$时,$y = - 5$;当$x = 6$时,$y = - 2$。
将$\begin{cases}x = - 3\\y = - 5\end{cases}$和$\begin{cases}x = 6\\y = - 2\end{cases}$分别代入$y = kx + b$中,得到方程组$\begin{cases}-3k + b = - 5\\6k + b = - 2\end{cases}$。
用第二个方程$6k + b = - 2$减去第一个方程$-3k + b = - 5$,可得:
$\begin{aligned}(6k + b) - (-3k + b)&=-2 - (-5)\\6k + b + 3k - b&=-2 + 5\\9k&=3\\k&=\frac{1}{3}\end{aligned}$
把$k = \frac{1}{3}$代入$-3k + b = - 5$,可得:
$\begin{aligned}-3×\frac{1}{3} + b&=- 5\\-1 + b&=- 5\\b&=- 5 + 1\\b&=- 4\end{aligned}$
此时函数解析式为$y = \frac{1}{3}x - 4$。
- **当$k\lt0$时:**
一次函数$y = kx + b$中$y$随$x$的增大而减小。
已知自变量的取值范围是$-3\leq x\leq6$,相应函数值的取值范围是$-5\leq y\leq - 2$,所以当$x = - 3$时,$y = - 2$;当$x = 6$时,$y = - 5$。
将$\begin{cases}x = - 3\\y = - 2\end{cases}$和$\begin{cases}x = 6\\y = - 5\end{cases}$分别代入$y = kx + b$中,得到方程组$\begin{cases}-3k + b = - 2\\6k + b = - 5\end{cases}$。
用第二个方程$6k + b = - 5$减去第一个方程$-3k + b = - 2$,可得:
$\begin{aligned}(6k + b) - (-3k + b)&=-5 - (-2)\\6k + b + 3k - b&=-5 + 2\\9k&=-3\\k&=-\frac{1}{3}\end{aligned}$
把$k = -\frac{1}{3}$代入$-3k + b = - 2$,可得:
$\begin{aligned}-3×(-\frac{1}{3}) + b&=- 2\\1 + b&=- 2\\b&=- 2 - 1\\b&=- 3\end{aligned}$
此时函数解析式为$y = -\frac{1}{3}x - 3$。
综上,这个函数的解析式为$y = \frac{1}{3}x - 4$或$y = -\frac{1}{3}x - 3$。
【答案】:$y = \frac{1}{3}x - 4$或$y = -\frac{1}{3}x - 3$
查看更多完整答案,请扫码查看


