《2025年假期园地暑假作业八年级数学人教版》

1. 人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下：$\overline {x}_{甲}= \overline {x}_{乙}= 80$,$s^{2}_{甲}= 240$,$s^{2}_{乙}= 180$,则成绩较为稳定的班级是(B)
A.甲班
B.乙班
C.两班成绩一样稳定
D.无法确定

答案： B

2. 若$x^{2}-x-2= 0$,则$\frac {x^{2}-x+2\sqrt {3}}{(x^{2}-x)^{2}-1+\sqrt {3}}$的值等于(A)
A.$\frac {2\sqrt {3}}{3}$
B.$\frac {\sqrt {3}}{3}$
C.$\sqrt {3}$
D.$\sqrt {3}或\frac {\sqrt {3}}{3}$

答案： A

3. 已知直线$y= (k-2)x+k$不经过第三象限,则$k$的取值范围是(D)
A.$k≠2$
B.$k＞2$
C.$0\lt k＜2$
D.$0≤k≤2$

答案： D

4. 方程$|4x-8|+\sqrt {x-y-m}= 0$,当$y＞0$时,$m$的取值范围是$m\lt2$.

答案： $m\lt2$

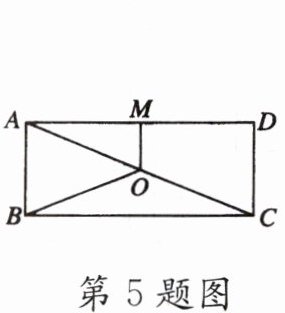
5. 如图,$O是矩形ABCD的对角线AC$的中点,$M是AD$的中点,若$AB= 5$,$AD= 12$,则四边形$ABOM$的周长为______20.

答案： $20$

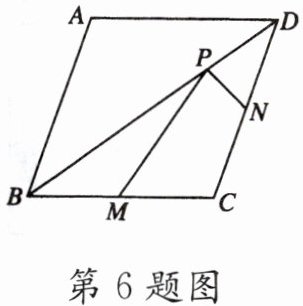
6. 如图,已知菱形$ABCD的两条对角线分别为6和8$,$M$,$N分别是边BC$,$CD$的中点,$P是对角线BD$上一点,则$PM+PN$的最小值是5.

答案： $5$

7. 计算：$(π-3)^{0}-|\sqrt {5}-3|+(-\frac {1}{3})^{-2}-\sqrt {5}$.

答案： 【解析】：本题可根据零指数幂、负整数指数幂、绝对值的性质以及根式的运算法则来逐步计算。
**步骤一：计算$(\pi - 3)^0$的值**
根据零指数幂的运算法则：任何非零数的$0$次幂都等于$1$，因为$\pi\approx3.14\gt3$，所以$\pi - 3\neq0$，则$(\pi - 3)^0 = 1$。
**步骤二：化简$\vert\sqrt{5} - 3\vert$的值**
因为$\sqrt{5}\approx2.24\lt3$，所以$\sqrt{5} - 3\lt0$。
根据绝对值的性质：当$a\lt0$时，$\vert a\vert = -a$，可得$\vert\sqrt{5} - 3\vert = -( \sqrt{5} - 3)= 3 - \sqrt{5}$。
**步骤三：计算$(-\frac{1}{3})^{-2}$的值**
根据负整数指数幂的运算法则：$a^{-p}=\frac{1}{a^p}$（$a\neq0$，$p$为正整数），可得$(-\frac{1}{3})^{-2}=\frac{1}{(-\frac{1}{3})^2}=\frac{1}{\frac{1}{9}} = 9$。
**步骤四：将上述结果代入原式进行计算**
$\begin{aligned}&(\pi - 3)^0 - \vert\sqrt{5} - 3\vert + (-\frac{1}{3})^{-2} - \sqrt{5}\\=&1 - (3 - \sqrt{5}) + 9 - \sqrt{5}\\=&1 - 3 + \sqrt{5} + 9 - \sqrt{5}\\=&(1 + 9 - 3)+(\sqrt{5} - \sqrt{5})\\=&7 + 0\\=&7\end{aligned}$
【答案】：$7$