《2025年假期园地暑假作业八年级数学人教版》

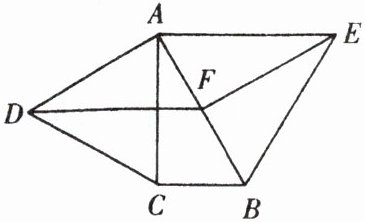
8. 如图,分别以 $ \mathrm { Rt } \triangle A B C $ 的直角边 $ A C $ 及斜边 $ A B $ 向外作等边三角形 $ A C D $,等边三角形 $ A B E $,已知 $ \angle B A C = 30 ^ { \circ } $,$ E F \perp A B $,垂足为 $ F $,连接 $ D F $.
(1)试证明：$ A C = E F $；
证明：因为$\triangle ABE$是等边三角形，$EF\perp AB$，所以$\angle AEF=\frac{1}{2}\angle AEB = 30^{\circ}$，$AE = AB$，$\angle EFA = 90^{\circ}$。又因为$\angle BAC = 30^{\circ}$，$\angle ACB = 90^{\circ}$，所以$\angle EFA=\angle ACB$。在$\triangle ABC$和$\triangle EAF$中，$\left\{\begin{array}{l}\angle ACB=\angle EFA\\\angle BAC=\angle AEF\\AB = EA\end{array}\right.$，根据$AAS$可得$\triangle ABC\cong\triangle EAF$，所以$AC = EF$。
(2)求证：四边形 $ A D F E $ 是平行四边形.
证明：因为$\triangle ACD$是等边三角形，所以$\angle DAC = 60^{\circ}$，$AC = AD$。由(1)知$AC = EF$，所以$AD = EF$。因为$\angle BAC = 30^{\circ}$，所以$\angle DAB=\angle DAC+\angle BAC=60^{\circ}+30^{\circ}=90^{\circ}$，又$\angle EFA = 90^{\circ}$，所以$AD// EF$。因为$AD// EF$且$AD = EF$，所以四边形$ADFE$是平行四边形。

答案： 【解析】：
(1) 因为$\triangle ABE$是等边三角形，$EF\perp AB$，所以$\angle AEF=\frac{1}{2}\angle AEB = 30^{\circ}$，$AE = AB$，$\angle EFA = 90^{\circ}$。
又因为$\angle BAC = 30^{\circ}$，$\angle ACB = 90^{\circ}$，所以$\angle EFA=\angle ACB$。
在$\triangle ABC$和$\triangle EAF$中，$\left\{\begin{array}{l}\angle ACB=\angle EFA\\\angle BAC=\angle AEF\\AB = EA\end{array}\right.$，根据$AAS$（两角及其中一角的对边对应相等的两个三角形全等）可得$\triangle ABC\cong\triangle EAF$，所以$AC = EF$。
(2) 因为$\triangle ACD$是等边三角形，所以$\angle DAC = 60^{\circ}$，$AC = AD$。
由
(1)知$AC = EF$，所以$AD = EF$。
因为$\angle BAC = 30^{\circ}$，所以$\angle DAB=\angle DAC+\angle BAC=60^{\circ}+30^{\circ}=90^{\circ}$，又$\angle EFA = 90^{\circ}$，所以$AD// EF$。
一组对边平行且相等的四边形是平行四边形，因为$AD// EF$且$AD = EF$，所以四边形$ADFE$是平行四边形。
【答案】：
(1) 证明见上述解析；
(2) 证明见上述解析。

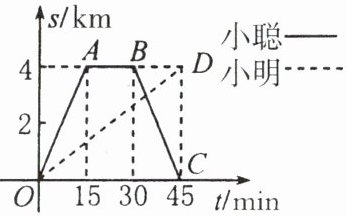
9. 小聪和小明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是 $ 4 \mathrm { km } $. 小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆. 图中折线 $ O - A - B - C $ 和线段 $ O D $ 分别表示两人离学校的路程 $ s ( \mathrm { km } ) $ 与所经过的时间 $ t ( \mathrm { min } ) $ 之间的函数关系,请根据图象回答下列问题：

(1)小聪在图书馆查阅资料的时间为______15$ \mathrm { min } $,小聪返回学校的速度为______$\frac{4}{15}$$ \mathrm { km } / \mathrm { min } $；
(2)请你求出小明离开学校的路程 $ s ( \mathrm { km } ) $ 与所经过的时间 $ t ( \mathrm { min } ) $ 之间的函数关系式；
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米？

答案： 【解析】：
### $(1)$计算小聪在图书馆查阅资料的时间和返回学校的速度
查阅资料时间：小聪到达图书馆（$A$点）时间是$15\mathrm{min}$，离开图书馆（$B$点）时间是$30\mathrm{min}$，所以查阅资料时间为$30 - 15=15\mathrm{min}$。
返回速度：小聪返回路程$s = 4\mathrm{km}$，返回时间$t=45 - 30 = 15\mathrm{min}$，根据速度公式$v=\frac{s}{t}$，可得返回速度$v=\frac{4}{15}\mathrm{km/min}$。
### $(2)$求小明离开学校的路程$s$与时间$t$的函数关系式
设$s$与$t$的函数关系式为$s = kt(k\neq0)$。
已知小明$45\mathrm{min}$走了$4\mathrm{km}$，把$(45,4)$代入$s = kt$得：$4 = 45k$，解得$k=\frac{4}{45}$。
所以$s$与$t$的函数关系式为$s=\frac{4}{45}t(0\leq t\leq45)$。
### $(3)$求小聪与小明迎面相遇时离学校的路程
小聪返回时（$30\leq t\leq45$），设$s$与$t$的函数关系式为$s=- \frac{4}{15}t + b$。
把$(30,4)$代入$s=- \frac{4}{15}t + b$得：$4=-\frac{4}{15}×30 + b$，
$4=- 8 + b$，解得$b = 12$，所以$s=- \frac{4}{15}t + 12(30\leq t\leq45)$。
当小聪与小明迎面相遇时，$\frac{4}{45}t=- \frac{4}{15}t + 12$，
$\frac{4}{45}t+\frac{12}{45}t = 12$，$\frac{16}{45}t = 12$，$t=\frac{135}{4}$。
把$t = \frac{135}{4}$代入$s=\frac{4}{45}t$得：$s=\frac{4}{45}×\frac{135}{4}=3\mathrm{km}$。
【答案】：
$(1)$$\boldsymbol{15}$，$\boldsymbol{\frac{4}{15}}$；
$(2)$$\boldsymbol{s=\frac{4}{45}t(0\leq t\leq45)}$；
$(3)$$\boldsymbol{3}$千米。