2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6. 先化简,再求值:
$(\frac {a^{2}-5a+2}{a+2}+1)÷\frac {a^{2}-4}{a^{2}+4a+4}$,其中$a= 2+\sqrt {3}$。
$(\frac {a^{2}-5a+2}{a+2}+1)÷\frac {a^{2}-4}{a^{2}+4a+4}$,其中$a= 2+\sqrt {3}$。
答案:
【解析】:
本题可先对原式进行化简,再将$a$的值代入化简后的式子求值。
### 步骤一:化简原式
- **化简$(\frac{a^2 - 5a + 2}{a + 2} + 1)$:**
先对括号内的式子进行通分,再计算:
$\frac{a^2 - 5a + 2}{a + 2} + 1=\frac{a^2 - 5a + 2}{a + 2} + \frac{a + 2}{a + 2}=\frac{a^2 - 5a + 2 + a + 2}{a + 2}=\frac{a^2 - 4a + 4}{a + 2}$
根据完全平方公式$(m-n)^2=m^2-2mn+n^2$,对分子进一步化简可得$\frac{(a - 2)^2}{a + 2}$。
- **化简$\frac{a^2 - 4}{a^2 + 4a + 4}$:**
根据平方差公式$m^2-n^2=(m+n)(m-n)$,可得$a^2 - 4=(a + 2)(a - 2)$;
根据完全平方公式$(m+n)^2=m^2+2mn+n^2$,可得$a^2 + 4a + 4=(a + 2)^2$。
所以$\frac{a^2 - 4}{a^2 + 4a + 4}=\frac{(a + 2)(a - 2)}{(a + 2)^2}=\frac{a - 2}{a + 2}$。
- **计算除法:**
将上述化简结果代入原式,可得:
$(\frac{a^2 - 5a + 2}{a + 2} + 1)÷\frac{a^2 - 4}{a^2 + 4a + 4}=\frac{(a - 2)^2}{a + 2}÷\frac{a - 2}{a + 2}$
根据除法运算法则,除以一个数等于乘以它的倒数,则有:
$\frac{(a - 2)^2}{a + 2}÷\frac{a - 2}{a + 2}=\frac{(a - 2)^2}{a + 2}×\frac{a + 2}{a - 2}=a - 2$
### 步骤二:代入求值
将$a = 2 + \sqrt{3}$代入化简后的式子$a - 2$,可得:
$2 + \sqrt{3} - 2=\sqrt{3}$
【答案】:$\sqrt{3}$
本题可先对原式进行化简,再将$a$的值代入化简后的式子求值。
### 步骤一:化简原式
- **化简$(\frac{a^2 - 5a + 2}{a + 2} + 1)$:**
先对括号内的式子进行通分,再计算:
$\frac{a^2 - 5a + 2}{a + 2} + 1=\frac{a^2 - 5a + 2}{a + 2} + \frac{a + 2}{a + 2}=\frac{a^2 - 5a + 2 + a + 2}{a + 2}=\frac{a^2 - 4a + 4}{a + 2}$
根据完全平方公式$(m-n)^2=m^2-2mn+n^2$,对分子进一步化简可得$\frac{(a - 2)^2}{a + 2}$。
- **化简$\frac{a^2 - 4}{a^2 + 4a + 4}$:**
根据平方差公式$m^2-n^2=(m+n)(m-n)$,可得$a^2 - 4=(a + 2)(a - 2)$;
根据完全平方公式$(m+n)^2=m^2+2mn+n^2$,可得$a^2 + 4a + 4=(a + 2)^2$。
所以$\frac{a^2 - 4}{a^2 + 4a + 4}=\frac{(a + 2)(a - 2)}{(a + 2)^2}=\frac{a - 2}{a + 2}$。
- **计算除法:**
将上述化简结果代入原式,可得:
$(\frac{a^2 - 5a + 2}{a + 2} + 1)÷\frac{a^2 - 4}{a^2 + 4a + 4}=\frac{(a - 2)^2}{a + 2}÷\frac{a - 2}{a + 2}$
根据除法运算法则,除以一个数等于乘以它的倒数,则有:
$\frac{(a - 2)^2}{a + 2}÷\frac{a - 2}{a + 2}=\frac{(a - 2)^2}{a + 2}×\frac{a + 2}{a - 2}=a - 2$
### 步骤二:代入求值
将$a = 2 + \sqrt{3}$代入化简后的式子$a - 2$,可得:
$2 + \sqrt{3} - 2=\sqrt{3}$
【答案】:$\sqrt{3}$
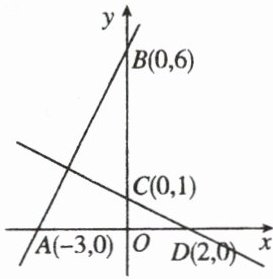
7. 如图所示,点A,B,C,D的坐标如图,求直线AB与直线CD的交点坐标。

(-2,2)
答案:
【解析】:
设直线$AB$的解析式为$y = k_1x + b_1$,将$A(-3,0)$,$B(0,6)$代入可得:
$\begin{cases}-3k_1 + b_1 = 0 \\ b_1 = 6\end{cases}$
解得$\begin{cases}k_1 = 2 \\ b_1 = 6\end{cases}$
所以直线$AB$的解析式为$y = 2x + 6$。
设直线$CD$的解析式为$y = k_2x + b_2$,将$C(0,1)$,$D(2,0)$代入可得:
$\begin{cases}b_2 = 1 \\ 2k_2 + b_2 = 0\end{cases}$
解得$\begin{cases}k_2 = -\frac{1}{2} \\ b_2 = 1\end{cases}$
所以直线$CD$的解析式为$y = -\frac{1}{2}x + 1$。
联立直线$AB$与直线$CD$的解析式可得:
$\begin{cases}y = 2x + 6 \\ y = -\frac{1}{2}x + 1\end{cases}$
即$2x + 6 = -\frac{1}{2}x + 1$
$2x+\frac{1}{2}x=1 - 6$
$\frac{5}{2}x=-5$
$x = -2$
将$x = -2$代入$y = 2x + 6$得$y = 2×(-2)+6 = 2$。
【答案】:$(-2,2)$
设直线$AB$的解析式为$y = k_1x + b_1$,将$A(-3,0)$,$B(0,6)$代入可得:
$\begin{cases}-3k_1 + b_1 = 0 \\ b_1 = 6\end{cases}$
解得$\begin{cases}k_1 = 2 \\ b_1 = 6\end{cases}$
所以直线$AB$的解析式为$y = 2x + 6$。
设直线$CD$的解析式为$y = k_2x + b_2$,将$C(0,1)$,$D(2,0)$代入可得:
$\begin{cases}b_2 = 1 \\ 2k_2 + b_2 = 0\end{cases}$
解得$\begin{cases}k_2 = -\frac{1}{2} \\ b_2 = 1\end{cases}$
所以直线$CD$的解析式为$y = -\frac{1}{2}x + 1$。
联立直线$AB$与直线$CD$的解析式可得:
$\begin{cases}y = 2x + 6 \\ y = -\frac{1}{2}x + 1\end{cases}$
即$2x + 6 = -\frac{1}{2}x + 1$
$2x+\frac{1}{2}x=1 - 6$
$\frac{5}{2}x=-5$
$x = -2$
将$x = -2$代入$y = 2x + 6$得$y = 2×(-2)+6 = 2$。
【答案】:$(-2,2)$
8. 某校为了了解学生做课外作业所用时间的情况,对学生做课外作业所用时间进行调查,下表是该校八年级某班50名学生某一天做数学课外作业所用时间的情况统计表:
|所用时间t/分|人数|
|$0<t≤10$|4|
|$10<t≤20$|6|
|$20<t≤30$|14|
|$30<t≤40$|13|
|$40<t≤50$|9|
|$50<t≤60$|4|
(1)第二组数据的组中值是______
(2)求该班学生平均每天做数学作业所用的时间。
|所用时间t/分|人数|
|$0<t≤10$|4|
|$10<t≤20$|6|
|$20<t≤30$|14|
|$30<t≤40$|13|
|$40<t≤50$|9|
|$50<t≤60$|4|
(1)第二组数据的组中值是______
15
;(2)求该班学生平均每天做数学作业所用的时间。
30.8分
答案:
【解析】:
(1)组中值是指各组上限与下限之间的中点数值。对于第二组$10\lt t\leqslant20$,其组中值为$\frac{10 + 20}{2}=15$。
(2)要求该班学生平均每天做数学作业所用的时间,需要先确定每组的组中值,再利用加权平均数公式$\overline{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots +x_{n}f_{n}}{f_{1}+f_{2}+\cdots +f_{n}}$来计算,其中$x_{i}$是组中值,$f_{i}$是该组的频数。
第一组$0\lt t\leqslant10$的组中值为$\frac{0 + 10}{2}=5$;
第二组$10\lt t\leqslant20$的组中值为$\frac{10 + 20}{2}=15$;
第三组$20\lt t\leqslant30$的组中值为$\frac{20 + 30}{2}=25$;
第四组$30\lt t\leqslant40$的组中值为$\frac{30 + 40}{2}=35$;
第五组$40\lt t\leqslant50$的组中值为$\frac{40 + 50}{2}=45$;
第六组$50\lt t\leqslant60$的组中值为$\frac{50 + 60}{2}=55$。
则该班学生平均每天做数学作业所用的时间为:
$\begin{aligned}\overline{x}&=\frac{5×4 + 15×6+25×14 + 35×13+45×9+55×4}{4 + 6+14 + 13+9+4}\\&=\frac{20+90 + 350+455+405+220}{50}\\&=\frac{1540}{50}\\& = 30.8(分)\end{aligned}$
【答案】:(1)15;(2)30.8分
(1)组中值是指各组上限与下限之间的中点数值。对于第二组$10\lt t\leqslant20$,其组中值为$\frac{10 + 20}{2}=15$。
(2)要求该班学生平均每天做数学作业所用的时间,需要先确定每组的组中值,再利用加权平均数公式$\overline{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots +x_{n}f_{n}}{f_{1}+f_{2}+\cdots +f_{n}}$来计算,其中$x_{i}$是组中值,$f_{i}$是该组的频数。
第一组$0\lt t\leqslant10$的组中值为$\frac{0 + 10}{2}=5$;
第二组$10\lt t\leqslant20$的组中值为$\frac{10 + 20}{2}=15$;
第三组$20\lt t\leqslant30$的组中值为$\frac{20 + 30}{2}=25$;
第四组$30\lt t\leqslant40$的组中值为$\frac{30 + 40}{2}=35$;
第五组$40\lt t\leqslant50$的组中值为$\frac{40 + 50}{2}=45$;
第六组$50\lt t\leqslant60$的组中值为$\frac{50 + 60}{2}=55$。
则该班学生平均每天做数学作业所用的时间为:
$\begin{aligned}\overline{x}&=\frac{5×4 + 15×6+25×14 + 35×13+45×9+55×4}{4 + 6+14 + 13+9+4}\\&=\frac{20+90 + 350+455+405+220}{50}\\&=\frac{1540}{50}\\& = 30.8(分)\end{aligned}$
【答案】:(1)15;(2)30.8分
查看更多完整答案,请扫码查看


