2025年假期园地暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若$x - y = \sqrt{2} - 1$,$xy = \sqrt{2}$,则代数式$(x - 1)(y + 1)$的值等于(
A.$2\sqrt{2} + 2$
B.$2\sqrt{2} - 2$
C.$2\sqrt{2}$
D.$2$
B
)A.$2\sqrt{2} + 2$
B.$2\sqrt{2} - 2$
C.$2\sqrt{2}$
D.$2$
答案:
B
2. 如图,在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,$AB = 3$,$BC = 4$,点$D在BC$上,以$AC为对角线的所有□ ADCE$中,$DE$最小的值是(

A.$2$
B.$3$
C.$4$
D.$5$
B
)
A.$2$
B.$3$
C.$4$
D.$5$
答案:
B
3. 如图,边长为$6$的大正方形中有两个小正方形,若两个小正方形的面积分别为$S_{1}$,$S_{2}$,则$S_{1} + S_{2}$的值为(
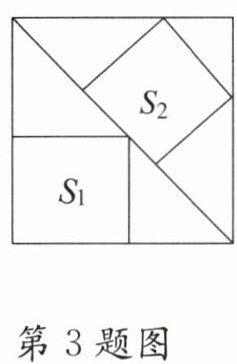
A.$16$
B.$17$
C.$18$
D.$19$
B
)
A.$16$
B.$17$
C.$18$
D.$19$
答案:
B
4. 若$y = x^{a + 2}$是正比例函数,则$a$的值是______
-1
。
答案:
$-1$
5. 已知一次函数$y = 2x - 6与y = -x + 3的图象交于点P$,则点$P$的坐标为
$(3,0)$
。
答案:
$(3,0)$
6. 汽车开始行驶时油箱内有油$40$升,如果每小时耗油$5$升,则油箱内余油量$Q$升与行驶时间$t$小时的关系是
$Q = 40 - 5t$
。
答案:
$Q = 40 - 5t$
7. 解不等式:$\sqrt{2}(x - \sqrt{3}) \geq \sqrt{6}(x + 1)$。
答案:
【解析】:
本题可先去括号,再移项、合并同类项,最后将系数化为$1$来求解不等式。
- **步骤一:去括号**
根据乘法分配律$a(b+c)=ab+ac$,将不等式$\sqrt{2}(x - \sqrt{3}) \geq \sqrt{6}(x + 1)$两边的括号去掉,可得:
$\sqrt{2}x - \sqrt{6} \geq \sqrt{6}x + \sqrt{6}$
- **步骤二:移项**
把含有$x$的项移到不等式左边,常数项移到不等式右边,移项时要注意变号,得到:
$\sqrt{2}x - \sqrt{6}x \geq \sqrt{6} + \sqrt{6}$
- **步骤三:合并同类项**
对不等式左边的$\sqrt{2}x - \sqrt{6}x$提取公因式$x$可得$(\sqrt{2} - \sqrt{6})x$,对不等式右边的$\sqrt{6} + \sqrt{6}$合并同类项可得$2\sqrt{6}$,此时不等式变为:
$(\sqrt{2} - \sqrt{6})x \geq 2\sqrt{6}$
- **步骤四:系数化为$1$**
因为$\sqrt{2}-\sqrt{6}\lt0$,根据不等式的性质:不等式两边同时除以同一个负数,不等号的方向改变,所以在不等式$(\sqrt{2} - \sqrt{6})x \geq 2\sqrt{6}$两边同时除以$\sqrt{2} - \sqrt{6}$,不等号方向改变,得到:
$x\leq\frac{2\sqrt{6}}{\sqrt{2} - \sqrt{6}}$
为了将分母有理化,给$\frac{2\sqrt{6}}{\sqrt{2} - \sqrt{6}}$的分子分母同时乘以$\sqrt{2} + \sqrt{6}$,可得:
$\begin{aligned}x&\leq\frac{2\sqrt{6}(\sqrt{2} + \sqrt{6})}{(\sqrt{2} - \sqrt{6})(\sqrt{2} + \sqrt{6})}\\&=\frac{2\sqrt{12}+2×6}{(\sqrt{2})^2 - (\sqrt{6})^2}\\&=\frac{4\sqrt{3}+12}{2 - 6}\\&=\frac{4\sqrt{3}+12}{-4}\\&=-\sqrt{3}-3\end{aligned}$
【答案】:$x\leq - 3 - \sqrt{3}$
本题可先去括号,再移项、合并同类项,最后将系数化为$1$来求解不等式。
- **步骤一:去括号**
根据乘法分配律$a(b+c)=ab+ac$,将不等式$\sqrt{2}(x - \sqrt{3}) \geq \sqrt{6}(x + 1)$两边的括号去掉,可得:
$\sqrt{2}x - \sqrt{6} \geq \sqrt{6}x + \sqrt{6}$
- **步骤二:移项**
把含有$x$的项移到不等式左边,常数项移到不等式右边,移项时要注意变号,得到:
$\sqrt{2}x - \sqrt{6}x \geq \sqrt{6} + \sqrt{6}$
- **步骤三:合并同类项**
对不等式左边的$\sqrt{2}x - \sqrt{6}x$提取公因式$x$可得$(\sqrt{2} - \sqrt{6})x$,对不等式右边的$\sqrt{6} + \sqrt{6}$合并同类项可得$2\sqrt{6}$,此时不等式变为:
$(\sqrt{2} - \sqrt{6})x \geq 2\sqrt{6}$
- **步骤四:系数化为$1$**
因为$\sqrt{2}-\sqrt{6}\lt0$,根据不等式的性质:不等式两边同时除以同一个负数,不等号的方向改变,所以在不等式$(\sqrt{2} - \sqrt{6})x \geq 2\sqrt{6}$两边同时除以$\sqrt{2} - \sqrt{6}$,不等号方向改变,得到:
$x\leq\frac{2\sqrt{6}}{\sqrt{2} - \sqrt{6}}$
为了将分母有理化,给$\frac{2\sqrt{6}}{\sqrt{2} - \sqrt{6}}$的分子分母同时乘以$\sqrt{2} + \sqrt{6}$,可得:
$\begin{aligned}x&\leq\frac{2\sqrt{6}(\sqrt{2} + \sqrt{6})}{(\sqrt{2} - \sqrt{6})(\sqrt{2} + \sqrt{6})}\\&=\frac{2\sqrt{12}+2×6}{(\sqrt{2})^2 - (\sqrt{6})^2}\\&=\frac{4\sqrt{3}+12}{2 - 6}\\&=\frac{4\sqrt{3}+12}{-4}\\&=-\sqrt{3}-3\end{aligned}$
【答案】:$x\leq - 3 - \sqrt{3}$
查看更多完整答案,请扫码查看


