《2025年Happy暑假作业快乐暑假武汉大学出版社八年级数学通用版》

15. (★★★)某企业急需一辆汽车,但无资金购买,公司经理决定租一辆汽车,使用期限为一个月。甲汽车出租公司的出租条件为每千米的租车费为 1.2 元,乙汽车出租公司的条件是每月须支付司机 800 元的工资,另外每千米的租车费为 1 元,设在这一个月中汽车行驶 $ x ( \mathrm { km } ) $,租用甲公司汽车的费用为 $ y _ { 1 } $(元),租用乙公司汽车的费用为 $ y _ { 2 } $(元)。
(1)试分别写出 $ y _ { 1 } $,$ y _ { 2 } $ 与 $ x $ 之间的函数关系式；
(2)当汽车行驶路程为多少千米时,租用乙公司的汽车合算？

答案： 1. $y_1 = 1.2x$，$y_2 = 800 + x$
2. 当汽车行驶路程大于$4000$千米时，租用乙公司的汽车合算。

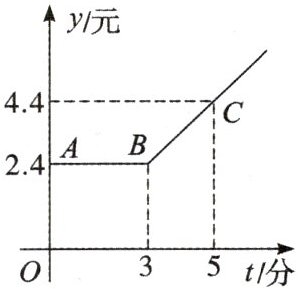
16. (★★★)如图所示,折线 $ A B C $ 表示从甲地向乙地打长途电话所需的电话费 $ y $(元)与通话时间 $ t $(分)之间的函数关系的图象。
(1)写出 $ y $ 与 $ t $ 之间的函数关系式；
(2)通话 2 分钟应付通话费多少元？通话 7 分钟呢？

答案：
(1)$y=\begin{cases}2.4(0\lt t\leqslant3)\\t - 0.6(t\gt3)\end{cases}$
(2)通话$2$分钟应付通话费$2.4$元，通话$7$分钟应付通话费$6.4$元。

17. (★★★★)某工厂现有甲种原料 $ 360 \mathrm { kg } $,乙种原料 $ 290 \mathrm { kg } $,计划利用这两种原料生产 $ \mathrm { A } $,$ \mathrm { B } $ 两种产品,共 50 件。已知生产一件 $ \mathrm { A } $ 种产品需用甲种原料 $ 9 \mathrm { kg } $、乙种原料 $ 3 \mathrm { kg } $,可获利润 700 元；生产一件 $ \mathrm { B } $ 种产品,需用甲种原料 $ 4 \mathrm { kg } $、乙种原料 $ 10 \mathrm { kg } $,可获利润 1 200 元。
(1)要求安排 $ \mathrm { A } $,$ \mathrm { B } $ 两种产品的生产件数,有哪几种方案？请你设计出来；
(2)生产 $ \mathrm { A } $,$ \mathrm { B } $ 两种产品获得的总利润是 $ y $(元),其中一种的生产件数是 $ x $,试写出 $ y $ 与 $ x $ 之间的函数关系式,并利用函数的性质说明(1)中的哪种生产方案获总利润最大？最大利润是多少？

答案： 1. 有三种方案：方案一：生产$A$种产品$30$件，$B$种产品$20$件；方案二：生产$A$种产品$31$件，$B$种产品$19$件；方案三：生产$A$种产品$32$件，$B$种产品$18$件。
2. $y=-500x + 60000$（$x$为生产$A$种产品的件数）；方案一获总利润最大，最大利润是$45000$元。