《2025年Happy暑假作业快乐暑假武汉大学出版社八年级数学通用版》

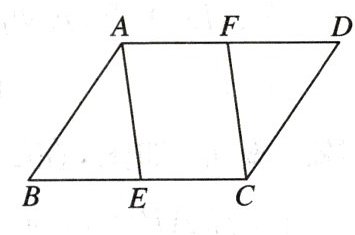
16. (★★)平行四边形$ABCD$中,点$E$,$F分别在BC$,$AD$上,且$AF = CE$,求证:$AE = CF$.

答案： 因为四边形$ABCD$是平行四边形，所以$AD// BC$，即$AF// CE$。又$AF = CE$，所以四边形$AECF$是平行四边形（一组对边平行且相等的四边形是平行四边形），所以$AE = CF$（平行四边形的对边相等）。

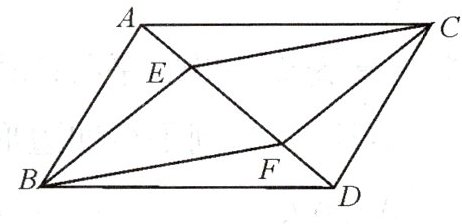
17. (★★★)已知:如图,在平行四边形$ABDC$中,点$E$,$F在AD$上,且$AE = DF$,求证:四边形$BECF$是平行四边形.

答案： $\because$四边形$ABDC$是平行四边形，$\therefore AB = DC$，$AB// DC$，$\therefore\angle BAE=\angle CDF$。
在$\triangle ABE$和$\triangle DCF$中，$\begin{cases}AB = DC\\\angle BAE=\angle CDF\\AE = DF\end{cases}$，$\therefore\triangle ABE\cong\triangle DCF(SAS)$，$\therefore BE = CF$。
$\because AE = DF$，$\therefore AE + EF=DF + EF$，即$AF = DE$。
又$\because AB = DC$，$AB// DC$，$\therefore\angle BAF=\angle CDE$。
在$\triangle BED$和$\triangle CFA$中，$\begin{cases}AB = DC\\\angle BAF=\angle CDE\\AF = DE\end{cases}$，$\therefore\triangle BED\cong\triangle CFA(SAS)$，$\therefore CF = BE$。
$\because BE = CF$，$CF = BE$，$\therefore$四边形$BECF$是平行四边形（两组对边分别相等的四边形是平行四边形）。