《2025年一本预备新高一数学》

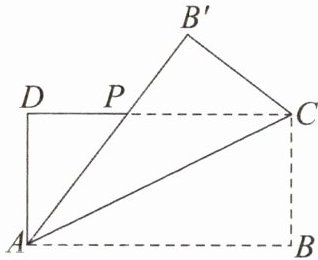
【变式2】如图,矩形ABCD(AB＞BC)的周长为24,把它沿AC翻折,翻折后AB'交DC于点P,设AB= x.
(1)用含x的式子表示DP的长,并直接写出x的取值范围;
(2)用含x的式子表示△ADP的面积,并求出△ADP面积的最大值及此时x的值.

答案： 解：
(1)$\because$ 矩形 $ ABCD(AB ＞ BC) $ 的周长为 24，$ AB = x $，
$\therefore AD = 12 - x $。由题意，得 $ AP = PC $，$ AB' = CD $，则 $ DP = PB' $，$\therefore AP = AB' - PB' = AB - DP = x - DP $。
由 $ AB ＞ BC = AD $，得 $ x ＞ 12 - x $，$\therefore 6 ＜ x ＜ 12 $。
在 $ Rt\triangle ADP $ 中，由勾股定理，得 $ (12 - x)^2 + DP^2 = (x - DP)^2 $，
$\therefore DP = 12 - \frac{72}{x}(6 ＜ x ＜ 12)$。
(2)由题意，得 $ S_{\triangle ADP} = \frac{1}{2}AD \cdot DP = \frac{1}{2}(12 - x) \cdot (12 - \frac{72}{x}) = 108 - (6x + \frac{432}{x})(6 ＜ x ＜ 12) $。
由基本不等式，得 $ 6x + \frac{432}{x} \geq 2\sqrt{6x \cdot \frac{432}{x}} = 72\sqrt{2} $，当且仅当 $ 6x = \frac{432}{x} $，即 $ x = 6\sqrt{2} $ 时，等号成立，即 $ S_{\triangle ADP} = 108 - (6x + \frac{432}{x}) \leq 108 - 72\sqrt{2} $，故 $ \triangle ADP $ 面积的最大值为 $ 108 - 72\sqrt{2} $，此时 $ x $ 的值为 $ 6\sqrt{2} $。

1.某公司一年需要购买某种原材料400t,计划每次购买x t.已知每次的运费为4万元,一年总的库存费用为4x万元,为了使总费用最低,每次购买的数量x为 ()
A.20
B.23
C.25
D.28

答案： A 由题意，得一年的总费用为 $ 4 \cdot \frac{400}{x} + 4x = \frac{1600}{x} + 4x \geq 2\sqrt{\frac{1600}{x} \cdot 4x} = 160 $，当且仅当 $ \frac{1600}{x} = 4x $，即 $ x = 20 $ 时，等号成立，所以为了使总费用最低，每次购买的数量 $ x $ 为 20。

2.如果两个正方形的边长之和为1,那么它们的面积之和的最小值是 ()
A.1/4
B.1/2
C.1
D.2

答案： B 设两个正方形的边长分别为 $ a $，$ b $，则 $ a + b = 1 $，$ a ＞ 0 $，$ b ＞ 0 $，$\therefore 2\sqrt{ab} \leq a + b = 1 $，当且仅当 $ a = b = \frac{1}{2} $ 时，等号成立，$\therefore ab \leq \frac{1}{4} $，$\therefore a^2 + b^2 = (a + b)^2 - 2ab = 1 - 2ab \geq 1 - \frac{1}{2} = \frac{1}{2} $。

3.为净化水质,向一个游泳池加入某种化学药品,加入药品后池水中该药品的浓度C(单位:mg/L)随时间t(单位:h)的变化关系为$C= 20t/(t^2+4),$则经过______h后,池水中该药品的浓度达到最大.

答案： 2 $ C = \frac{20t}{t^2 + 4} = \frac{20}{t + \frac{4}{t}} \leq \frac{20}{2\sqrt{t \cdot \frac{4}{t}}} = 5 $，当且仅当 $ t = \frac{4}{t} $，即 $ t = 2 $ 时，等号成立，因此经过 2 h 后，池水中该药品的浓度达到最大。

4.(教材改编题)要制作一个容积为$4m^3,$高为1m的无盖长方体容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是______.

答案： 160 元 设底面长方形的长、宽分别为 $ x $，$ y $，则 $ xy = 4 $，$ S_{\text{侧}} = 2x + 2y = 2x + \frac{8}{x} $，所以总造价 $ z = 20xy + 10 \times (2x + \frac{8}{x}) = 80 + 20x + \frac{80}{x} \geq 80 + 2\sqrt{20x \cdot \frac{80}{x}} = 160 $，当且仅当 $ 20x = \frac{80}{x} $，即 $ x = 2 $ 时，等号成立，故该容器的最低总造价是 160 元。