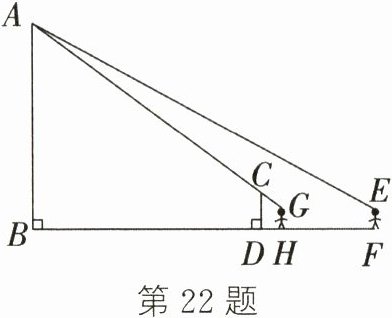
22. (10分)如图,某楼的高度AB = 18.2米,小华在距该楼30米(FB = 30米)的点F处,沿FB向点B前进,当走到点H处时,恰好看到广告牌CD的顶端C和楼顶A在一条直线上,小华的眼睛到地面的距离EF = GH = 1.7米,广告牌的高度CD = 3.2米,BD = 20米,点B,D,H,F在同一水平线上,AB⊥BF,CD⊥BF,GH⊥BF,EF⊥BF. 求小华从点F处向前走了多少米恰好看到点C和点A在一条直线上(即求HF的长).

答案:
如图,过点$G$作$GM\perp AB$于点$M$,交$CD$于点$N$. 易得四边形$MBDN$,四边形$MBHG$,四边形$NDHG$为矩形,$\therefore AB// CD$,$NG = DH$,$MB = ND = GH = 1.7$米,$MN = BD = 20$米. $\therefore CN = CD - ND = 1.5$米,$AM = AB - MB = 16.5$米. $\because AB// CD$,$\therefore \triangle AMG\sim\triangle CNG$. $\therefore \frac{AM}{CN}=\frac{MG}{NG}$,即$\frac{16.5}{1.5}=\frac{20 + NG}{NG}$. $\therefore NG = 2$米. $\therefore DH = NG = 2$米. $\therefore HF = BF - BD - DH = 30 - 20 - 2 = 8$(米). $\therefore$小华从点$F$处向前走了$8$米恰好看到点$C$和点$A$在一条直线上
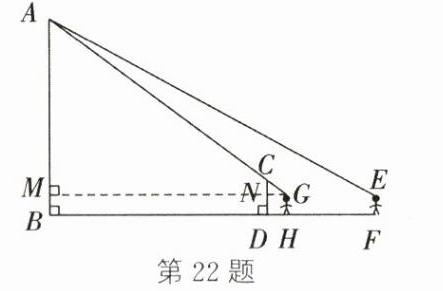
如图,过点$G$作$GM\perp AB$于点$M$,交$CD$于点$N$. 易得四边形$MBDN$,四边形$MBHG$,四边形$NDHG$为矩形,$\therefore AB// CD$,$NG = DH$,$MB = ND = GH = 1.7$米,$MN = BD = 20$米. $\therefore CN = CD - ND = 1.5$米,$AM = AB - MB = 16.5$米. $\because AB// CD$,$\therefore \triangle AMG\sim\triangle CNG$. $\therefore \frac{AM}{CN}=\frac{MG}{NG}$,即$\frac{16.5}{1.5}=\frac{20 + NG}{NG}$. $\therefore NG = 2$米. $\therefore DH = NG = 2$米. $\therefore HF = BF - BD - DH = 30 - 20 - 2 = 8$(米). $\therefore$小华从点$F$处向前走了$8$米恰好看到点$C$和点$A$在一条直线上

23. (12分)
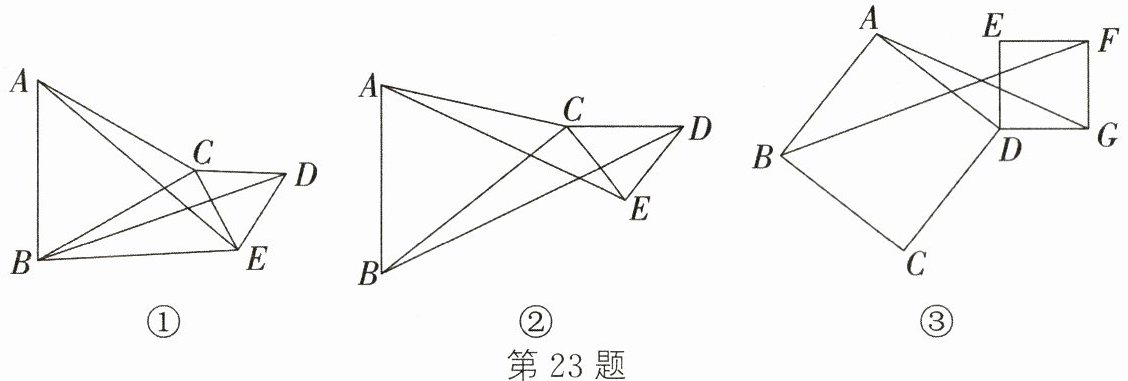
(1)如图①,△ABC和△EDC都是等边三角形,则BD_______AE(填“>”“<”或“=”);
(2)如图②,在△ABC和△EDC中,AB = AC = 4,BC = 5,EC = ED,∠BAC = ∠CED = α,探究AE和BD之间的数量关系;
(3)如图③,在正方形ABCD和正方形DEFG中,探究BF和AG之间的数量关系.
(1)如图①,△ABC和△EDC都是等边三角形,则BD_______AE(填“>”“<”或“=”);
(2)如图②,在△ABC和△EDC中,AB = AC = 4,BC = 5,EC = ED,∠BAC = ∠CED = α,探究AE和BD之间的数量关系;
(3)如图③,在正方形ABCD和正方形DEFG中,探究BF和AG之间的数量关系.

答案:
(1)$=$ (2)$\because AB = AC$,$EC = ED$,$\angle BAC=\angle CED=\alpha$,$\therefore \angle ABC=\angle ACB=\angle ECD=\angle EDC=\frac{1}{2}(180^{\circ}-\alpha)$. $\therefore \triangle ABC\sim\triangle EDC$. $\therefore \frac{AC}{EC}=\frac{BC}{DC}$,即$\frac{AC}{BC}=\frac{EC}{DC}$. 又$\because \angle ACB+\angle BCE=\angle ECD+\angle BCE$,即$\angle ACE=\angle BCD$,$\therefore \triangle ACE\sim\triangle BCD$. $\therefore \frac{AE}{BD}=\frac{AC}{BC}=\frac{4}{5}$ (3)如图,连接$BD$,$DF$. $\because$四边形$ABCD$和四边形$DEFG$都是正方形,$\therefore AB = AD$,$\angle BAD = 90^{\circ}$,$DG = GF$,$\angle DGF = 90^{\circ}$. $\therefore \angle ADB=\angle ABD=\angle GDF=\angle GFD = 45^{\circ}$. 在$Rt\triangle BAD$中,由勾股定理,得$BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{AD^{2}+AD^{2}}=\sqrt{2}AD$,$\therefore \frac{BD}{AD}=\sqrt{2}$. 同理,可得$\frac{DF}{DG}=\sqrt{2}$,$\therefore \frac{BD}{AD}=\frac{DF}{DG}$. $\because \angle ADB=\angle GDF$,$\therefore \angle ADB+\angle ADF=\angle GDF+\angle ADF$,即$\angle BDF=\angle ADG$. $\therefore \triangle BDF\sim\triangle ADG$. $\therefore \frac{BF}{AG}=\frac{BD}{AD}=\sqrt{2}$
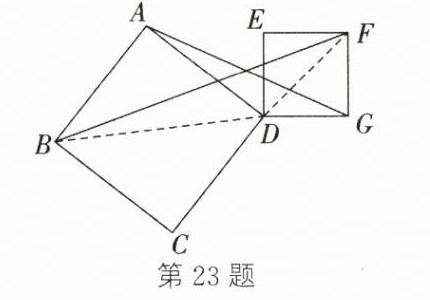
(1)$=$ (2)$\because AB = AC$,$EC = ED$,$\angle BAC=\angle CED=\alpha$,$\therefore \angle ABC=\angle ACB=\angle ECD=\angle EDC=\frac{1}{2}(180^{\circ}-\alpha)$. $\therefore \triangle ABC\sim\triangle EDC$. $\therefore \frac{AC}{EC}=\frac{BC}{DC}$,即$\frac{AC}{BC}=\frac{EC}{DC}$. 又$\because \angle ACB+\angle BCE=\angle ECD+\angle BCE$,即$\angle ACE=\angle BCD$,$\therefore \triangle ACE\sim\triangle BCD$. $\therefore \frac{AE}{BD}=\frac{AC}{BC}=\frac{4}{5}$ (3)如图,连接$BD$,$DF$. $\because$四边形$ABCD$和四边形$DEFG$都是正方形,$\therefore AB = AD$,$\angle BAD = 90^{\circ}$,$DG = GF$,$\angle DGF = 90^{\circ}$. $\therefore \angle ADB=\angle ABD=\angle GDF=\angle GFD = 45^{\circ}$. 在$Rt\triangle BAD$中,由勾股定理,得$BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{AD^{2}+AD^{2}}=\sqrt{2}AD$,$\therefore \frac{BD}{AD}=\sqrt{2}$. 同理,可得$\frac{DF}{DG}=\sqrt{2}$,$\therefore \frac{BD}{AD}=\frac{DF}{DG}$. $\because \angle ADB=\angle GDF$,$\therefore \angle ADB+\angle ADF=\angle GDF+\angle ADF$,即$\angle BDF=\angle ADG$. $\therefore \triangle BDF\sim\triangle ADG$. $\therefore \frac{BF}{AG}=\frac{BD}{AD}=\sqrt{2}$

查看更多完整答案,请扫码查看


