21.(12分)研究发现:初中生在数学课上的听课注意力指标随上课时间的变化而变化,指标达到36为认真听讲,注意力指标$y$随时间$x$(单位:min)变化的函数图象如图所示. 当$0\leq x < 10$或$10\leq x < 20$时,图象是线段;当$20\leq x\leq 45$时,图象是反比例函数图象的一部分.
(1)求点$A$对应的指标;
(2)李老师在课上讲一道数学题需要17 min,他能否经过适当安排,使学生在认真听讲时进行讲解?

(1)求点$A$对应的指标;
(2)李老师在课上讲一道数学题需要17 min,他能否经过适当安排,使学生在认真听讲时进行讲解?

答案:
(1)当 $20\leqslant x\leqslant45$ 时,设反比例函数的解析式为 $y = \frac{k}{x}$。将 $C(20,45)$ 代入,得 $45=\frac{k}{20}$,解得 $k = 900$。$\therefore$ 反比例函数的解析式为 $y=\frac{900}{x}(20\leqslant x\leqslant45)$。把 $x = 45$ 代入 $y=\frac{900}{x}$,得 $y = 20$,$\therefore$ 点 $D$ 的坐标为 $(45,20)$。$\therefore$ 点 $A$ 的坐标为 $(0,20)$,即点 $A$ 对应的指标为 $20$ (2)当 $0\leqslant x\lt10$ 时,设线段 $AB$ 对应的函数解析式为 $y = mx + n$。把 $A(0,20)$,$B(10,45)$ 代入,得 $\begin{cases}n = 20\\10m + n = 45\end{cases}$,解得 $\begin{cases}m=\frac{5}{2}\\n = 20\end{cases}$。$\therefore$ 线段 $AB$ 对应的函数解析式为 $y=\frac{5}{2}x + 20(0\leqslant x\lt10)$。在 $y=\frac{5}{2}x + 20$ 中,当 $y\geqslant36$ 时,$\frac{5}{2}x + 20\geqslant36$,解得 $x\geqslant\frac{32}{5}$。当 $10\leqslant x\lt20$ 时,$y = 45\gt36$。在 $y=\frac{900}{x}$ 中,当 $y\geqslant36$ 时,$\frac{900}{x}\geqslant36$,解得 $0\lt x\leqslant25$。$\therefore$ 当 $\frac{32}{5}\leqslant x\leqslant25$ 时,注意力指标不低于 $36$。$\because$ 指标达到 $36$ 为认真听讲,而 $25-\frac{32}{5}=\frac{93}{5}\gt17$,$\therefore$ 李老师能经过适当安排,使学生在认真听讲时进行讲解
22.(15分)(济南中考)如图,一次函数$y = \frac{1}{2}x + 1$的图象与反比例函数$y = \frac{k}{x}(x > 0)$的图象交于点$A(a,3)$,与$y$轴交于点$B$.
(1)求$a$,$k$的值.
(2)直线$CD$过点$A$,与反比例函数$y = \frac{k}{x}(x > 0)$的图象交于点$C$,与$x$轴交于点$D$,$AC = AD$,连接$CB$.
① 求$\triangle ABC$的面积;
② 点$P$在反比例函数$y = \frac{k}{x}(x > 0)$的图象上,点$Q$在$x$轴上,若以点$A$,$B$,$P$,$Q$为顶点的四边形是平行四边形,请求出所有符合条件的点$P$的坐标.

(1)求$a$,$k$的值.
(2)直线$CD$过点$A$,与反比例函数$y = \frac{k}{x}(x > 0)$的图象交于点$C$,与$x$轴交于点$D$,$AC = AD$,连接$CB$.
① 求$\triangle ABC$的面积;
② 点$P$在反比例函数$y = \frac{k}{x}(x > 0)$的图象上,点$Q$在$x$轴上,若以点$A$,$B$,$P$,$Q$为顶点的四边形是平行四边形,请求出所有符合条件的点$P$的坐标.

答案:
(1)把 $A(a,3)$ 代入 $y=\frac{1}{2}x + 1$,得 $\frac{1}{2}a + 1 = 3$,解得 $a = 4$。$\therefore$ 点 $A$ 的坐标为 $(4,3)$。把 $A(4,3)$ 代入 $y=\frac{k}{x}$,得 $3=\frac{k}{4}$,解得 $k = 12$ (2)① 如图①,过点 $A$ 作 $AM\perp x$ 轴于点 $M$,过点 $C$ 作 $CT\perp x$ 轴于点 $T$,$CT$ 交 $AB$ 于点 $E$,过点 $A$ 作 $AN\perp CT$ 于点 $N$,则 $\angle ANC=\angle CTD=\angle DMA = 90^{\circ}$。$\therefore AN// x$ 轴。$\therefore\angle CAN=\angle ADM$。在 $\triangle ACN$ 和 $\triangle DAM$ 中,$\begin{cases}\angle ANC=\angle DMA\\\angle CAN=\angle ADM\\AC = DA\end{cases}$,$\therefore\triangle ACN\cong\triangle DAM$。$\therefore CN = AM$。$\because AN// x$ 轴,$CT\perp x$ 轴,$AM\perp x$ 轴,$\therefore AM = NT$。$\because A(4,3)$,$\therefore AM = NT = CN = 3$。$\therefore$ 点 $C$ 的纵坐标是 $6$。把 $y = 6$ 代入 $y=\frac{12}{x}$,得 $6=\frac{12}{x}$,解得 $x = 2$。$\therefore$ 点 $C$ 的坐标为 $(2,6)$。把 $x = 2$ 代入 $y=\frac{1}{2}x + 1$,得 $y = 2$,$\therefore$ 点 $E$ 的坐标为 $(2,2)$。$\therefore CE = 6 - 2 = 4$。$\therefore S_{\triangle ABC}=\frac{1}{2}CE\cdot(x_{C}-x_{B})+\frac{1}{2}CE\cdot(x_{A}-x_{C})=\frac{1}{2}CE\cdot(x_{A}-x_{B})=\frac{1}{2}\times4\times4 = 8$ ② 把 $x = 0$ 代入 $y=\frac{1}{2}x + 1$,得 $y = 1$,$\therefore$ 点 $B$ 的坐标为 $(0,1)$。如图②,当 $AB$ 是对角线时,四边形 $APBQ$ 是平行四边形。$\because$ 点 $A$ 的坐标为 $(4,3)$,点 $B$ 的坐标为 $(0,1)$,点 $Q$ 的纵坐标为 $0$,$\therefore y_{P}=\frac{1 + 3}{2}\times2-0 = 4$。把 $y = 4$ 代入 $y=\frac{12}{x}$,得 $4=\frac{12}{x}$,解得 $x = 3$。$\therefore$ 点 $P$ 的坐标为 $(3,4)$。当 $AB$ 为边时,四边形 $ABQP$ 是平行四边形(图中的 $\square ABQ'P'$),$\therefore y_{P'}=\frac{3 + 0}{2}\times2-1 = 2$。把 $y = 2$ 代入 $y=\frac{12}{x}$,得 $2=\frac{12}{x}$,解得 $x = 6$。$\therefore$ 点 $P'$ 的坐标为 $(6,2)$。综上所述,点 $P$ 的坐标为 $(3,4)$ 或 $(6,2)$
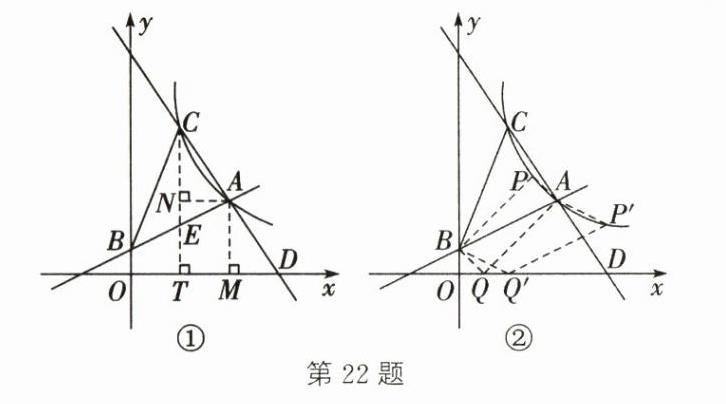
(1)把 $A(a,3)$ 代入 $y=\frac{1}{2}x + 1$,得 $\frac{1}{2}a + 1 = 3$,解得 $a = 4$。$\therefore$ 点 $A$ 的坐标为 $(4,3)$。把 $A(4,3)$ 代入 $y=\frac{k}{x}$,得 $3=\frac{k}{4}$,解得 $k = 12$ (2)① 如图①,过点 $A$ 作 $AM\perp x$ 轴于点 $M$,过点 $C$ 作 $CT\perp x$ 轴于点 $T$,$CT$ 交 $AB$ 于点 $E$,过点 $A$ 作 $AN\perp CT$ 于点 $N$,则 $\angle ANC=\angle CTD=\angle DMA = 90^{\circ}$。$\therefore AN// x$ 轴。$\therefore\angle CAN=\angle ADM$。在 $\triangle ACN$ 和 $\triangle DAM$ 中,$\begin{cases}\angle ANC=\angle DMA\\\angle CAN=\angle ADM\\AC = DA\end{cases}$,$\therefore\triangle ACN\cong\triangle DAM$。$\therefore CN = AM$。$\because AN// x$ 轴,$CT\perp x$ 轴,$AM\perp x$ 轴,$\therefore AM = NT$。$\because A(4,3)$,$\therefore AM = NT = CN = 3$。$\therefore$ 点 $C$ 的纵坐标是 $6$。把 $y = 6$ 代入 $y=\frac{12}{x}$,得 $6=\frac{12}{x}$,解得 $x = 2$。$\therefore$ 点 $C$ 的坐标为 $(2,6)$。把 $x = 2$ 代入 $y=\frac{1}{2}x + 1$,得 $y = 2$,$\therefore$ 点 $E$ 的坐标为 $(2,2)$。$\therefore CE = 6 - 2 = 4$。$\therefore S_{\triangle ABC}=\frac{1}{2}CE\cdot(x_{C}-x_{B})+\frac{1}{2}CE\cdot(x_{A}-x_{C})=\frac{1}{2}CE\cdot(x_{A}-x_{B})=\frac{1}{2}\times4\times4 = 8$ ② 把 $x = 0$ 代入 $y=\frac{1}{2}x + 1$,得 $y = 1$,$\therefore$ 点 $B$ 的坐标为 $(0,1)$。如图②,当 $AB$ 是对角线时,四边形 $APBQ$ 是平行四边形。$\because$ 点 $A$ 的坐标为 $(4,3)$,点 $B$ 的坐标为 $(0,1)$,点 $Q$ 的纵坐标为 $0$,$\therefore y_{P}=\frac{1 + 3}{2}\times2-0 = 4$。把 $y = 4$ 代入 $y=\frac{12}{x}$,得 $4=\frac{12}{x}$,解得 $x = 3$。$\therefore$ 点 $P$ 的坐标为 $(3,4)$。当 $AB$ 为边时,四边形 $ABQP$ 是平行四边形(图中的 $\square ABQ'P'$),$\therefore y_{P'}=\frac{3 + 0}{2}\times2-1 = 2$。把 $y = 2$ 代入 $y=\frac{12}{x}$,得 $2=\frac{12}{x}$,解得 $x = 6$。$\therefore$ 点 $P'$ 的坐标为 $(6,2)$。综上所述,点 $P$ 的坐标为 $(3,4)$ 或 $(6,2)$

查看更多完整答案,请扫码查看


