19. (6分)如图所示为小华利用软件在直角坐标系中画出的△ABC和它的位似图形△A₁B₁C₁(三角形的顶点都在格点上).
(1)在图中标出△ABC与△A₁B₁C₁的位似中心点M,并写出点M的坐标;
(2)若以点O为位似中心,请你在图中画出△A₁B₁C₁的位似图形△A₂B₂C₂(点A₁,B₁,C₁的对应点分别为A₂,B₂,C₂),且△A₁B₁C₁与△A₂B₂C₂的相似比为2(只画一个即可).
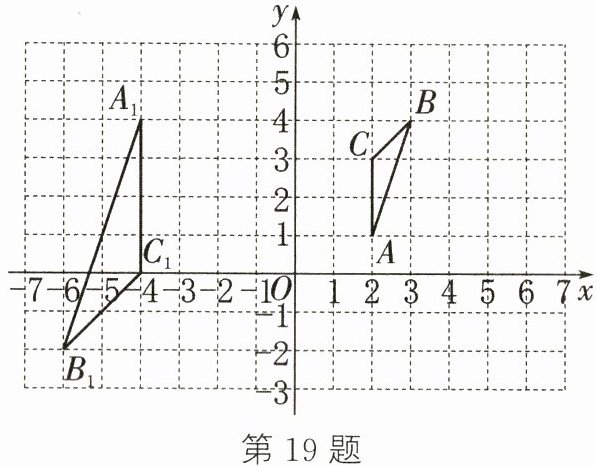
(1)在图中标出△ABC与△A₁B₁C₁的位似中心点M,并写出点M的坐标;
(2)若以点O为位似中心,请你在图中画出△A₁B₁C₁的位似图形△A₂B₂C₂(点A₁,B₁,C₁的对应点分别为A₂,B₂,C₂),且△A₁B₁C₁与△A₂B₂C₂的相似比为2(只画一个即可).

答案:
(1)如图,点$M$即为所求 点$M$的坐标为$(0,2)$ (2)答案不唯一,如图,$\triangle A_{2}B_{2}C_{2}$即为所求
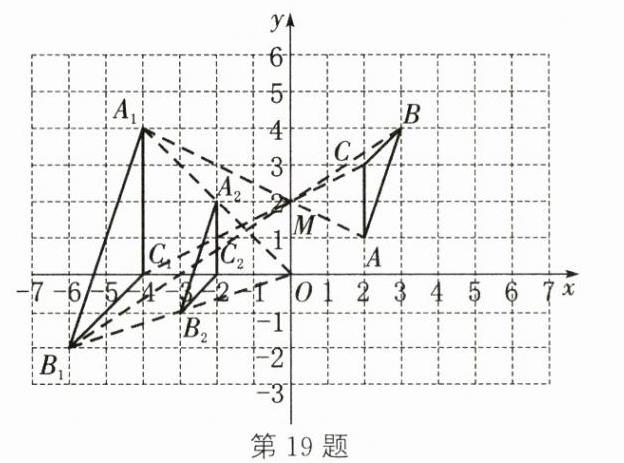
(1)如图,点$M$即为所求 点$M$的坐标为$(0,2)$ (2)答案不唯一,如图,$\triangle A_{2}B_{2}C_{2}$即为所求

20. (8分)如图,在△ABC中,AC的垂直平分线分别交AB,AC于点D,E,CD与BE交于点F,BC = BE.
(1)求证:△CFE∽△ABC;
(2)判断F是否为线段BE的中点,并说明理由.
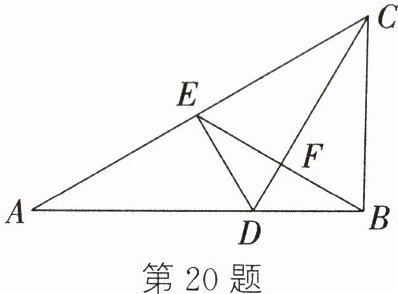
(1)求证:△CFE∽△ABC;
(2)判断F是否为线段BE的中点,并说明理由.

答案:
(1)$\because DE$垂直平分$AC$,$\therefore AD = CD$. $\therefore \angle ECF=\angle A$. $\because BC = BE$,$\therefore \angle CEF=\angle ACB$. $\therefore \triangle CFE\sim\triangle ABC$ (2)$F$为线段$BE$的中点 理由:$\because \triangle CFE\sim\triangle ABC$,$\therefore \frac{FE}{BC}=\frac{CE}{AC}$. $\because DE$垂直平分$AC$,$\therefore CE=\frac{1}{2}AC$. $\therefore \frac{CE}{AC}=\frac{1}{2}$. $\therefore \frac{FE}{BC}=\frac{1}{2}$. $\because BC = BE$,$\therefore \frac{FE}{BE}=\frac{1}{2}$. $\therefore F$为线段$BE$的中点.
21. (10分)(杭州中考)如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF,四边形BFED是平行四边形,且$\frac{DE}{BC}=\frac{1}{4}$.
(1)若AB = 8,求线段AD的长;
(2)若△ADE的面积为1,求□BFED的面积.
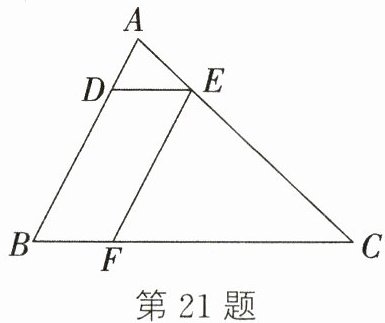
(1)若AB = 8,求线段AD的长;
(2)若△ADE的面积为1,求□BFED的面积.

答案:
(1)$\because$四边形$BFED$是平行四边形,$\therefore DE// BC$. $\therefore \triangle ADE\sim\triangle ABC$. $\therefore \frac{AD}{AB}=\frac{DE}{BC}=\frac{1}{4}$. $\because AB = 8$,$\therefore AD = 2$
(2)$\because \triangle ADE\sim\triangle ABC$,$\therefore \frac{DE}{BC}=\frac{AE}{AC}=\frac{1}{4}$,$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{DE}{BC})^{2}=(\frac{1}{4})^{2}=\frac{1}{16}$. $\because S_{\triangle ADE}=1$,$\therefore S_{\triangle ABC}=16$. $\because \frac{AE}{AC}=\frac{1}{4}$,$\therefore \frac{CE}{AC}=\frac{3}{4}$. $\because$四边形$BFED$是平行四边形,$\therefore EF// AB$. $\therefore \triangle EFC\sim\triangle ABC$. $\therefore \frac{S_{\triangle EFC}}{S_{\triangle ABC}}=(\frac{CE}{AC})^{2}=(\frac{3}{4})^{2}=\frac{9}{16}$. $\therefore S_{\triangle EFC}=9$. $\therefore S_{\square BFED}=S_{\triangle ABC}-S_{\triangle EFC}-S_{\triangle ADE}=16 - 9 - 1 = 6$
(2)$\because \triangle ADE\sim\triangle ABC$,$\therefore \frac{DE}{BC}=\frac{AE}{AC}=\frac{1}{4}$,$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{DE}{BC})^{2}=(\frac{1}{4})^{2}=\frac{1}{16}$. $\because S_{\triangle ADE}=1$,$\therefore S_{\triangle ABC}=16$. $\because \frac{AE}{AC}=\frac{1}{4}$,$\therefore \frac{CE}{AC}=\frac{3}{4}$. $\because$四边形$BFED$是平行四边形,$\therefore EF// AB$. $\therefore \triangle EFC\sim\triangle ABC$. $\therefore \frac{S_{\triangle EFC}}{S_{\triangle ABC}}=(\frac{CE}{AC})^{2}=(\frac{3}{4})^{2}=\frac{9}{16}$. $\therefore S_{\triangle EFC}=9$. $\therefore S_{\square BFED}=S_{\triangle ABC}-S_{\triangle EFC}-S_{\triangle ADE}=16 - 9 - 1 = 6$
查看更多完整答案,请扫码查看


