20.(6分)如图,在方格纸中,$\triangle OAB$的顶点坐标分别为$O(0,0)$,$A(-2,-1)$,$B(-1,-3)$,$\triangle O_{1}A_{1}B_{1}$与$\triangle OAB$是以点$P$为位似中心的位似图形。
(1)在图中标出位似中心$P$的位置,并写出点$P$及点$B$的对应点$B_{1}$的坐标;
(2)以原点$O$为位似中心,在$x$轴下方画出$\triangle OA_{2}B_{2}$,使$\triangle OA_{2}B_{2}$与$\triangle OAB$位似,且相似比为2,并写出点$B$的对应点$B_{2}$的坐标;
(3)$\triangle OAB$的内部一点$M$的坐标为$(a,b)$,直接写出点$M$在$\triangle OA_{2}B_{2}$中的对应点$M_{2}$的坐标。
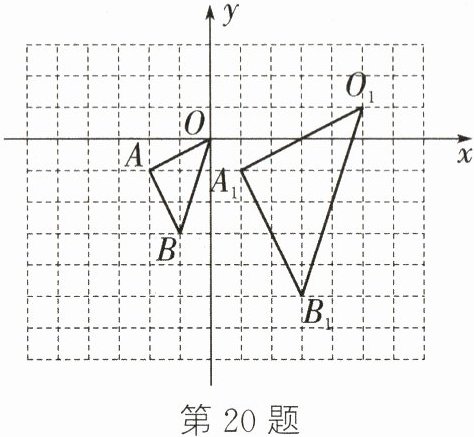
(1)在图中标出位似中心$P$的位置,并写出点$P$及点$B$的对应点$B_{1}$的坐标;
(2)以原点$O$为位似中心,在$x$轴下方画出$\triangle OA_{2}B_{2}$,使$\triangle OA_{2}B_{2}$与$\triangle OAB$位似,且相似比为2,并写出点$B$的对应点$B_{2}$的坐标;
(3)$\triangle OAB$的内部一点$M$的坐标为$(a,b)$,直接写出点$M$在$\triangle OA_{2}B_{2}$中的对应点$M_{2}$的坐标。

答案:
(1)如图,点$P$即为所求 $P(-5,-1)$,$B_{1}(3,-5)$ (2)如图,$\triangle OA_{2}B_{2}$即为所求 $B_{2}(-2,-6)$ (3)$M_{2}(2a,2b)$
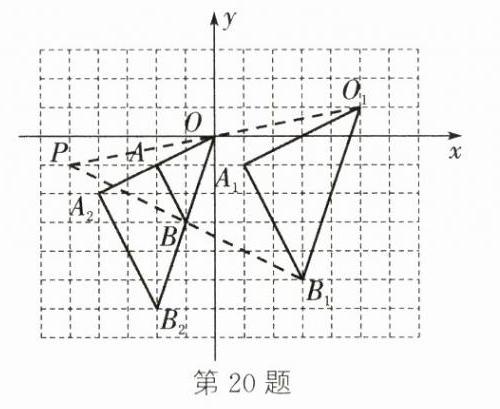
(1)如图,点$P$即为所求 $P(-5,-1)$,$B_{1}(3,-5)$ (2)如图,$\triangle OA_{2}B_{2}$即为所求 $B_{2}(-2,-6)$ (3)$M_{2}(2a,2b)$

21.(6分)某小队在探险过程中发现了一个深坑,小队人员为了测出深坑的深度,采取如下方案:如图,在深坑左侧用观测仪$AB$从观测出发点$A$观测深坑底部的点$P$,且观测视线刚好经过深坑边缘的点$M$,在深坑右侧用观测仪$CD$从观测出发点$C$观测深坑底部的点$P$,且观测视线刚好经过深坑边缘的点$N$(点$E$,$B$,$M$,$N$,$D$,$F$在同一水平线上)。已知$AB\perp EM$,$CD\perp NF$,观测仪$AB$高2 m,观测仪$CD$高1 m,$BM = 1.6$ m,$DN = 0.8$ m,深坑的宽度$MN = 8.8$ m,请根据以上数据计算深坑的深度。
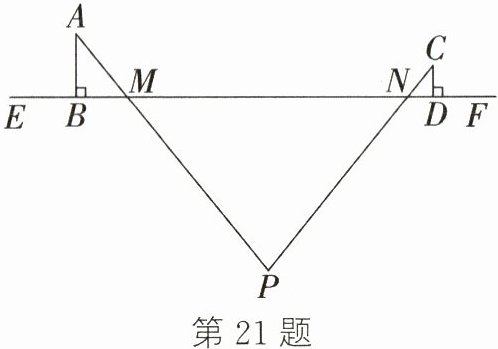

答案:
如图,过点$P$作$PH\perp EF$于点$H$。因为$AB\perp EF$,$PH\perp EF$,$CD\perp EF$,所以$\angle ABM=\angle PHM=\angle PHN=\angle CDN = 90^{\circ}$。又因为$\angle AMB=\angle PMH$,$\angle CND=\angle PNH$,所以$\triangle ABM\sim\triangle PHM$,$\triangle CDN\sim\triangle PHN$。所以$\frac{AB}{PH}=\frac{MB}{MH}$,$\frac{CD}{PH}=\frac{DN}{HN}$。所以$PH=\frac{AB\cdot MH}{MB}$,$PH=\frac{CD\cdot HN}{DN}$。所以$\frac{AB\cdot MH}{MB}=\frac{CD\cdot HN}{DN}$。由题意,得$AB = 2m$,$MB = 1.6m$,$CD = 1m$,$DN = 0.8m$,$MN = 8.8m$。设$MH = xm$,则$HN=(8.8 - x)m$,所以$\frac{2x}{1.6}=\frac{1\times(8.8 - x)}{0.8}$。所以$x = 4.4$。所以$PH=\frac{2\times4.4}{1.6}=5.5(m)$。所以深坑的深度为$5.5m$
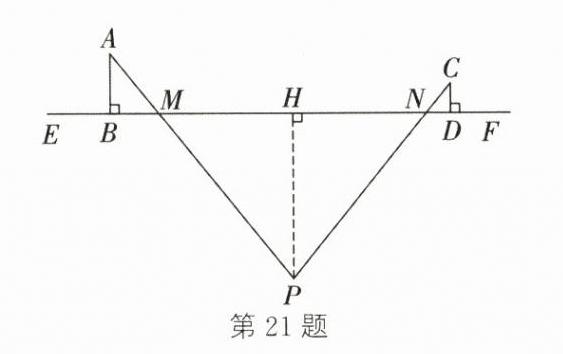
如图,过点$P$作$PH\perp EF$于点$H$。因为$AB\perp EF$,$PH\perp EF$,$CD\perp EF$,所以$\angle ABM=\angle PHM=\angle PHN=\angle CDN = 90^{\circ}$。又因为$\angle AMB=\angle PMH$,$\angle CND=\angle PNH$,所以$\triangle ABM\sim\triangle PHM$,$\triangle CDN\sim\triangle PHN$。所以$\frac{AB}{PH}=\frac{MB}{MH}$,$\frac{CD}{PH}=\frac{DN}{HN}$。所以$PH=\frac{AB\cdot MH}{MB}$,$PH=\frac{CD\cdot HN}{DN}$。所以$\frac{AB\cdot MH}{MB}=\frac{CD\cdot HN}{DN}$。由题意,得$AB = 2m$,$MB = 1.6m$,$CD = 1m$,$DN = 0.8m$,$MN = 8.8m$。设$MH = xm$,则$HN=(8.8 - x)m$,所以$\frac{2x}{1.6}=\frac{1\times(8.8 - x)}{0.8}$。所以$x = 4.4$。所以$PH=\frac{2\times4.4}{1.6}=5.5(m)$。所以深坑的深度为$5.5m$

查看更多完整答案,请扫码查看


