15. 如图,反比例函数$y_1 = \frac{k}{x}$的图象和一次函数$y_2 = ax + b$的图象交于$A(-1,2)$,$B(2,-1)$两点,则当$-2 < y_1 < y_2 < \frac{1}{2}$时,$x$的取值范围是___________.


答案:
$1\lt x\lt2$
16.(温州中考)在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强$p$(单位:kPa)与汽缸内气体的体积$V$(单位:mL)成反比例,$p$关于$V$的函数图象如图所示. 若压强由$75kPa$增加到$100kPa$,则气体的体积减少了_______mL.
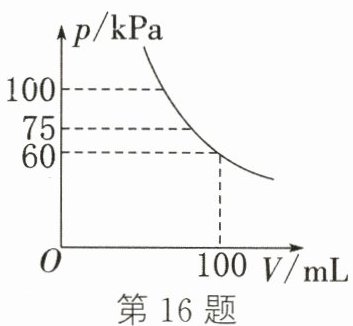

答案:
20
17. 对于反比例函数$y = - \frac{2}{x}$,当$0 < x \leq a$($a > 0$)时,$y \leq - 1$恒成立,则$a$的取值范围是_______.
答案:
$0\lt a\leqslant2$
18. 如图,在$\triangle OAB$中,点$A$在$y$轴上,反比例函数$y = \frac{k}{x}(x > 0)$的图象经过点$B$,并与$AB$交于点$C$. 若$BC = 2AC$,$S_{\triangle OAB} = 12$,则$k$的值为_______.


答案:
$-6$
19.(9分)反比例函数$y = \frac{4}{x}$的图象如图所示,一次函数$y = kx + b$的图象与反比例函数$y = \frac{4}{x}$的图象交于$A(m,4)$,$B(-2,n)$两点.
(1)求一次函数的解析式,并在所给的直角坐标系中画出该函数的图象;
(2)观察图象,直接写出不等式$kx + b < \frac{4}{x}$的解集.

(1)求一次函数的解析式,并在所给的直角坐标系中画出该函数的图象;
(2)观察图象,直接写出不等式$kx + b < \frac{4}{x}$的解集.

答案:
(1)$\because$ 点 $A(m,4)$,$B(-2,n)$ 在反比例函数 $y = \frac{4}{x}$ 的图象上,$\therefore 4m = 4$,$-2n = 4$,解得 $m = 1$,$n = -2$。$\therefore$ 点 $A$ 的坐标为 $(1,4)$,点 $B$ 的坐标为 $(-2,-2)$。把 $(1,4)$,$(-2,-2)$ 代入 $y = kx + b$,得 $\begin{cases}k + b = 4\\-2k + b = -2\end{cases}$,解得 $\begin{cases}k = 2\\b = 2\end{cases}$。$\therefore$ 一次函数的解析式为 $y = 2x + 2$。画出函数 $y = 2x + 2$ 的图象如图所示 (2)由图象可知,不等式 $2x + 2\lt\frac{4}{x}$ 的解集为 $x\lt - 2$ 或 $0\lt x\lt1$

(1)$\because$ 点 $A(m,4)$,$B(-2,n)$ 在反比例函数 $y = \frac{4}{x}$ 的图象上,$\therefore 4m = 4$,$-2n = 4$,解得 $m = 1$,$n = -2$。$\therefore$ 点 $A$ 的坐标为 $(1,4)$,点 $B$ 的坐标为 $(-2,-2)$。把 $(1,4)$,$(-2,-2)$ 代入 $y = kx + b$,得 $\begin{cases}k + b = 4\\-2k + b = -2\end{cases}$,解得 $\begin{cases}k = 2\\b = 2\end{cases}$。$\therefore$ 一次函数的解析式为 $y = 2x + 2$。画出函数 $y = 2x + 2$ 的图象如图所示 (2)由图象可知,不等式 $2x + 2\lt\frac{4}{x}$ 的解集为 $x\lt - 2$ 或 $0\lt x\lt1$

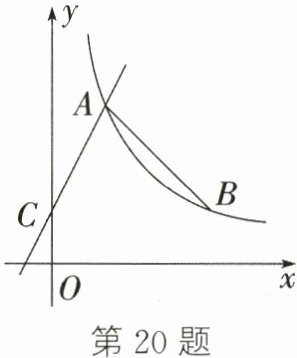
20.(10分)(乐山中考)如图,点$A(1,m)$,$B(n,1)$在反比例函数$y = \frac{3}{x}(x > 0)$的图象上,过点$A$的一次函数$y = kx + b$的图象与$y$轴交于点$C(0,1)$.
(1)求$m$,$n$的值和一次函数的解析式;
(2)连接$AB$,求点$C$到线段$AB$的距离.
(1)求$m$,$n$的值和一次函数的解析式;
(2)连接$AB$,求点$C$到线段$AB$的距离.

答案:
(1)$\because$ 点 $A(1,m)$,$B(n,1)$ 在反比例函数 $y = \frac{3}{x}$ 的图象上,$\therefore m = 3$,$n = 3$。又 $\because$ 一次函数 $y = kx + b$ 的图象过点 $A(1,3)$,$C(0,1)$,$\therefore\begin{cases}k + b = 3\\b = 1\end{cases}$,解得 $\begin{cases}k = 2\\b = 1\end{cases}$。$\therefore$ 一次函数的解析式为 $y = 2x + 1$ (2)如图,连接 $BC$,过点 $A$ 作 $AD\perp BC$,垂足为 $D$,过点 $C$ 作 $CE\perp AB$,垂足为 $E$。$\because C(0,1)$,$B(3,1)$,$\therefore BC// x$ 轴,$BC = 3$。$\because A(1,3)$,$B(3,1)$,$AD\perp BC$,$\therefore D(1,1)$,$AD = 2$,$BD = 2$。在 $Rt\triangle ADB$ 中,由勾股定理,得 $AB=\sqrt{AD^{2}+BD^{2}}=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$。$\because S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}AB\cdot CE$,即 $\frac{1}{2}\times3\times2=\frac{1}{2}\times2\sqrt{2}\times CE$,$\therefore CE=\frac{3\sqrt{2}}{2}$,即点 $C$ 到线段 $AB$ 的距离为 $\frac{3\sqrt{2}}{2}$

(1)$\because$ 点 $A(1,m)$,$B(n,1)$ 在反比例函数 $y = \frac{3}{x}$ 的图象上,$\therefore m = 3$,$n = 3$。又 $\because$ 一次函数 $y = kx + b$ 的图象过点 $A(1,3)$,$C(0,1)$,$\therefore\begin{cases}k + b = 3\\b = 1\end{cases}$,解得 $\begin{cases}k = 2\\b = 1\end{cases}$。$\therefore$ 一次函数的解析式为 $y = 2x + 1$ (2)如图,连接 $BC$,过点 $A$ 作 $AD\perp BC$,垂足为 $D$,过点 $C$ 作 $CE\perp AB$,垂足为 $E$。$\because C(0,1)$,$B(3,1)$,$\therefore BC// x$ 轴,$BC = 3$。$\because A(1,3)$,$B(3,1)$,$AD\perp BC$,$\therefore D(1,1)$,$AD = 2$,$BD = 2$。在 $Rt\triangle ADB$ 中,由勾股定理,得 $AB=\sqrt{AD^{2}+BD^{2}}=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$。$\because S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}AB\cdot CE$,即 $\frac{1}{2}\times3\times2=\frac{1}{2}\times2\sqrt{2}\times CE$,$\therefore CE=\frac{3\sqrt{2}}{2}$,即点 $C$ 到线段 $AB$ 的距离为 $\frac{3\sqrt{2}}{2}$

查看更多完整答案,请扫码查看


